How Many Edges Are In A Rectangular Prism
Juapaving
Mar 27, 2025 · 5 min read
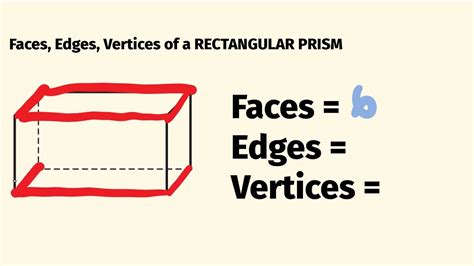
Table of Contents
How Many Edges Does a Rectangular Prism Have? A Comprehensive Exploration
The seemingly simple question, "How many edges does a rectangular prism have?" opens a door to a fascinating exploration of geometry, spatial reasoning, and the fundamental properties of three-dimensional shapes. While the answer itself is straightforward – 12 – understanding why a rectangular prism possesses this specific number of edges provides a deeper appreciation of its geometric characteristics. This article will delve into this question, exploring different approaches to counting edges, relating it to other geometric concepts, and considering variations and extensions of the problem.
Understanding Rectangular Prisms and Their Components
Before diving into edge counting, let's establish a firm understanding of what constitutes a rectangular prism. A rectangular prism, also known as a cuboid, is a three-dimensional geometric shape characterized by:
- Six rectangular faces: These faces are all parallelograms, meaning opposite sides are parallel and equal in length. In a rectangular prism, these parallelograms are specifically rectangles.
- Twelve edges: These are the line segments where two faces meet. They form the "skeleton" of the prism.
- Eight vertices: These are the points where three edges intersect. They are the corners of the prism.
Methodical Approaches to Counting Edges
There are several ways to systematically count the edges of a rectangular prism:
Method 1: Counting by Faces
Each rectangular face has four edges. Since there are six faces, a simple multiplication yields 6 faces * 4 edges/face = 24 edges. However, this overcounts. Each edge is shared by two faces. Therefore, we must divide by 2 to obtain the correct number: 24 edges / 2 = 12 edges.
Method 2: Counting by Vertex
Each vertex is the intersection point of three edges. A rectangular prism has eight vertices. If we simply multiplied 8 vertices * 3 edges/vertex = 24 edges, we would again overcount because each edge connects two vertices, resulting in each edge being counted twice. Thus, we divide by 2: 24 edges / 2 = 12 edges.
Method 3: Visualizing and Listing
A more intuitive approach is to systematically visualize and list the edges. We can imagine the rectangular prism and count the edges one by one. This method, while seemingly less efficient, can be beneficial for beginners to solidify their understanding of the shape's structure. We'd find four edges along the base, four vertical edges connecting the top and bottom faces, and four edges forming the top face. This leads to 4 + 4 + 4 = 12 edges. This method highlights the spatial arrangement of the edges.
Relating Edges to Other Geometric Properties
The number of edges in a rectangular prism is intrinsically linked to other geometric properties. For example:
-
Euler's Formula: Euler's formula for polyhedra (V - E + F = 2) relates the number of vertices (V), edges (E), and faces (F). For a rectangular prism: V = 8, F = 6, and E = 12. Substituting these values into Euler's formula confirms the relationship: 8 - 12 + 6 = 2.
-
Surface Area and Volume: While not directly related to the number of edges, the length of the edges is crucial in calculating the surface area and volume of a rectangular prism. The surface area is calculated using the lengths of the edges, and the volume involves the product of edge lengths. The edges define the dimensions of the prism.
-
Symmetry: A rectangular prism exhibits various symmetries. The number of edges and their arrangement contribute to these symmetries. The edges reflect the inherent symmetry within the shape.
Variations and Extensions
The concept of edges extends beyond rectangular prisms to other three-dimensional shapes:
- Cubes: A cube is a special case of a rectangular prism where all edges are equal in length. It still possesses 12 edges.
- Other Prisms: Other prisms, such as triangular prisms or pentagonal prisms, have a different number of edges depending on the shape of their bases. The number of edges increases with the number of sides in the base.
- Pyramids: Pyramids also have edges, but their number differs depending on the shape of the base. A square pyramid, for example, has 8 edges (4 from the base and 4 connecting the base to the apex).
Practical Applications and Real-World Examples
Understanding the number of edges, and the concept of edges in general, in a rectangular prism has practical applications in various fields:
-
Engineering and Architecture: Calculations involving rectangular prisms are commonplace in engineering and architectural design. Understanding the edge structure is crucial for structural analysis, material estimation, and building design.
-
Packaging and Logistics: Packaging often utilizes rectangular prisms. Knowing the number of edges helps in optimizing packaging design and efficient storage of goods.
-
Computer Graphics and 3D Modeling: In computer graphics and 3D modeling, rectangular prisms are fundamental building blocks. The edges define the shape and are used for rendering and manipulating 3D objects.
-
Game Development: Many games use rectangular prisms as basic elements in their environments or models. Accurate edge calculations are important for correct rendering and physics simulation.
Conclusion: More Than Just a Number
The seemingly simple question of how many edges a rectangular prism has reveals a deeper understanding of geometry and spatial reasoning. The twelve edges aren't just numerical abstractions; they are the defining structural elements that shape this fundamental geometric object. By approaching the question through various methods, relating it to other geometric properties, and exploring extensions to other shapes, we gain a richer appreciation for the mathematical principles governing three-dimensional shapes and their practical applications in the real world. The number 12, therefore, represents more than just a count; it symbolizes a gateway to a deeper comprehension of spatial relationships and geometric principles. From Euler's formula to real-world applications in engineering and design, the humble rectangular prism and its twelve edges offer a valuable lesson in the interconnectedness of mathematics and the physical world. Understanding this foundational concept is a crucial stepping stone towards mastering more complex geometric ideas and their practical applications across diverse fields.
Latest Posts
Latest Posts
-
Which Numbers Are Perfect Squares Check All That Apply
Mar 30, 2025
-
A Body Of Land Surrounded By Water On Three Sides
Mar 30, 2025
-
Is Square Root Of 15 An Irrational Number
Mar 30, 2025
-
When The Owner Withdraws Cash For Personal Use
Mar 30, 2025
-
What Is The Hybridization Of The Central Atom In Sf4
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about How Many Edges Are In A Rectangular Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
