Which Numbers Are Perfect Squares Check All That Apply
Juapaving
Mar 30, 2025 · 5 min read
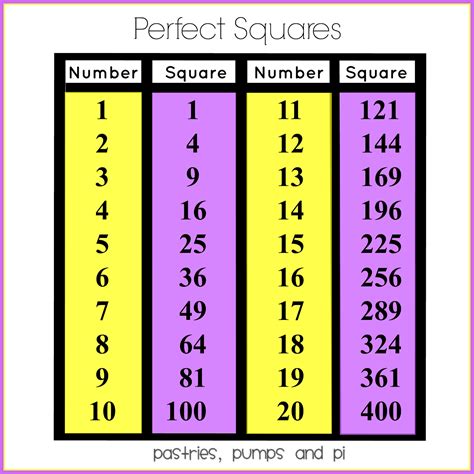
Table of Contents
Which Numbers Are Perfect Squares? Check All That Apply
Identifying perfect squares is a fundamental concept in mathematics with applications spanning various fields, from basic arithmetic to advanced algebra and geometry. Understanding perfect squares is crucial for simplifying expressions, solving equations, and grasping more complex mathematical concepts. This comprehensive guide will delve into the definition of perfect squares, provide methods for identifying them, and explore practical examples to solidify your understanding.
What is a Perfect Square?
A perfect square is a number that can be obtained by squaring (multiplying by itself) an integer. In simpler terms, it's the result of multiplying a whole number by itself. For example:
- 1 is a perfect square (1 x 1 = 1)
- 4 is a perfect square (2 x 2 = 4)
- 9 is a perfect square (3 x 3 = 9)
- 16 is a perfect square (4 x 4 = 16)
- And so on...
The integers that, when squared, produce the perfect square are called the square roots. Thus, the square root of 1 is 1, the square root of 4 is 2, the square root of 9 is 3, and so on.
It's important to note that perfect squares are always non-negative. You cannot obtain a negative number by squaring a real number.
Identifying Perfect Squares: Practical Techniques
Several methods can be used to identify whether a number is a perfect square. Here are some of the most effective:
1. Prime Factorization: A Systematic Approach
Prime factorization is a powerful technique for determining if a number is a perfect square. It involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). If, after prime factorization, every prime factor appears an even number of times, then the number is a perfect square.
Example: Let's consider the number 36.
-
Prime Factorization: 36 = 2 x 2 x 3 x 3 = 2² x 3²
-
Analysis: Both 2 and 3 appear twice (even number of times). Therefore, 36 is a perfect square (6 x 6 = 36).
Example: Now, let's consider the number 28.
-
Prime Factorization: 28 = 2 x 2 x 7 = 2² x 7
-
Analysis: While 2 appears twice, 7 appears only once (odd number of times). Therefore, 28 is not a perfect square.
2. Recognizing Patterns and Sequences: A Quick Check
With practice, you can quickly recognize many perfect squares. The first few perfect squares are: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400... Familiarity with these numbers allows for rapid identification in many cases.
Observe the differences between consecutive perfect squares:
- 4 - 1 = 3
- 9 - 4 = 5
- 16 - 9 = 7
- 25 - 16 = 9
- and so on...
Notice that the differences form an arithmetic sequence of odd numbers. This pattern can be helpful in quickly estimating whether a number might be a perfect square.
3. Using a Calculator or Software: A Convenient Option
Calculators and mathematical software packages offer a convenient way to determine if a number is a perfect square. Most calculators have a square root function (√). If the square root of a number is an integer, then the number is a perfect square.
For instance, if you input √144 into a calculator, you'll get 12, confirming that 144 is a perfect square.
Perfect Squares in Different Number Systems
The concept of perfect squares extends beyond the decimal system. Perfect squares can be found in other number systems, such as binary (base-2), hexadecimal (base-16), and others. The underlying principle remains the same: a number is a perfect square if it can be expressed as the square of an integer within the given number system.
For example, in binary:
- 1 (decimal) = 1 (binary) = 1²
- 4 (decimal) = 100 (binary) = 10² (in binary, 10 represents 2)
Applications of Perfect Squares
Perfect squares have wide-ranging applications across various mathematical fields and real-world scenarios. Here are a few examples:
- Geometry: Calculating the area of squares and other geometrical figures often involves perfect squares. The area of a square with side length 's' is s².
- Algebra: Solving quadratic equations frequently involves working with perfect squares to simplify expressions and find solutions.
- Number Theory: Perfect squares play a vital role in various number theory concepts, such as the study of Pythagorean triples and Diophantine equations.
- Computer Science: Perfect squares are used in algorithms and data structures, particularly in areas involving sorting and searching.
Identifying Perfect Squares: Practice Problems
Let's test your understanding with some practice problems:
- Is 121 a perfect square? (Yes, 11 x 11 = 121)
- Is 1000 a perfect square? (No, its prime factorization contains odd powers of primes)
- Is 625 a perfect square? (Yes, 25 x 25 = 625)
- Is 2025 a perfect square? (Yes, 45 x 45 = 2025)
- Is 441 a perfect square? (Yes, 21 x 21 = 441)
- Is 729 a perfect square? (Yes, 27 x 27 = 729)
- Is 1764 a perfect square? (Yes, 42 x 42 = 1764)
- Is 2401 a perfect square? (Yes, 49 x 49 = 2401)
- Is 3136 a perfect square? (Yes, 56 x 56 = 3136)
- Is 5041 a perfect square? (Yes, 71 x 71 = 5041)
Advanced Concepts: Beyond Basic Perfect Squares
While this guide focuses on the fundamentals of perfect squares, it's important to acknowledge the existence of more advanced concepts:
- Perfect square trinomials: These are trinomials (expressions with three terms) that can be factored into the square of a binomial. For example, x² + 6x + 9 = (x + 3)².
- Perfect square roots and their properties: Understanding the properties of square roots is essential for manipulating and simplifying algebraic expressions.
- Perfect squares in different number systems (as mentioned earlier): Extending the concept to other bases enriches your understanding of number systems.
Understanding perfect squares is a building block for many mathematical concepts. By mastering the techniques outlined in this guide and practicing regularly, you'll develop a strong foundation for more advanced mathematical explorations. Remember to utilize the various methods—prime factorization, pattern recognition, and calculator assistance—to efficiently identify perfect squares in diverse mathematical contexts.
Latest Posts
Latest Posts
-
Is Cellular Respiration Exergonic Or Endergonic
Apr 01, 2025
-
What Is The Gcf Of 12 And 30
Apr 01, 2025
-
Base Ten Numbers In Expanded Form
Apr 01, 2025
-
Why Do Biologists Assign Each Organism A Universally Accepted Name
Apr 01, 2025
-
Finding Area Under A Curve Calculator
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Which Numbers Are Perfect Squares Check All That Apply . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
