How Many Diagonals Does A Hexagon Have
Juapaving
Mar 26, 2025 · 5 min read
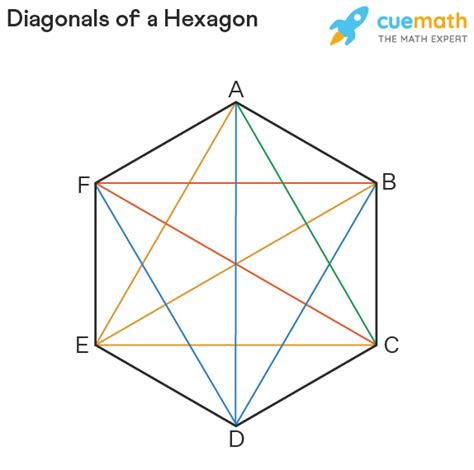
Table of Contents
- How Many Diagonals Does A Hexagon Have
- Table of Contents
- How Many Diagonals Does a Hexagon Have? A Comprehensive Guide
- Understanding Polygons and Diagonals
- The Hexagon: A Six-Sided Polygon
- Method 1: Visual Inspection and Counting
- Method 2: Using Combinatorics
- Understanding Combinations
- Applying Combinations to Diagonals
- Applying the Formula to the Hexagon
- Method 3: Systematic Approach and Pattern Recognition
- Practical Applications and Further Exploration
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
How Many Diagonals Does a Hexagon Have? A Comprehensive Guide
Determining the number of diagonals in a hexagon might seem like a simple geometry problem, but it opens the door to understanding more complex concepts in mathematics and offers a great opportunity to explore different approaches to problem-solving. This comprehensive guide will not only answer the question of how many diagonals a hexagon has but will also delve into the underlying principles, explore various methods for calculating the diagonals of polygons in general, and offer practical applications of this knowledge.
Understanding Polygons and Diagonals
Before we tackle the hexagon specifically, let's define some key terms. A polygon is a closed two-dimensional figure with three or more straight sides. Examples include triangles, squares, pentagons, hexagons, and so on. A diagonal of a polygon is a line segment connecting two non-adjacent vertices (corners) of the polygon. It's crucial to understand that a diagonal is inside the polygon; it doesn't extend beyond its perimeter.
The Hexagon: A Six-Sided Polygon
A hexagon is a polygon with six sides and six vertices. Regular hexagons have all sides and angles equal, but the number of diagonals remains the same regardless of whether the hexagon is regular or irregular. Our focus is on determining the number of diagonals regardless of the hexagon's specific shape.
Method 1: Visual Inspection and Counting
The simplest, albeit most time-consuming, method is to draw a hexagon and manually count its diagonals. Let's try this:
-
Draw a Hexagon: Draw a hexagon, labeling its vertices (corners) A, B, C, D, E, and F.
-
Identify the Diagonals: From each vertex, draw lines connecting to all non-adjacent vertices. For example, from vertex A, you can draw diagonals to C, D, and E. Avoid lines to B or F (those are sides, not diagonals).
-
Count the Diagonals: Carefully count all the diagonals you've drawn. You should find a total of nine diagonals.
This method works well for small polygons like hexagons but becomes impractical for polygons with many sides.
Method 2: Using Combinatorics
A more efficient and scalable method involves using combinations from combinatorics. This approach allows us to calculate the number of diagonals for any polygon, not just a hexagon.
Understanding Combinations
In combinatorics, a combination is a selection of items from a set where the order does not matter. We use the notation "n choose k" or ⁿCₖ, which is calculated as:
ⁿCₖ = n! / (k!(n-k)!)
Where:
- n is the total number of items in the set.
- k is the number of items chosen.
- ! denotes the factorial (e.g., 5! = 5 x 4 x 3 x 2 x 1).
Applying Combinations to Diagonals
For a polygon with n vertices, we can use combinations to calculate the number of diagonals as follows:
-
Total Number of Line Segments: First, we find the total number of line segments that can be formed by connecting any two vertices. This is given by ⁿC₂, which represents choosing 2 vertices out of n.
-
Number of Sides: Subtract the number of sides (n) from the total number of line segments. This is because the sides of the polygon are not considered diagonals.
Therefore, the formula for the number of diagonals in a polygon with n vertices is:
Number of diagonals = ⁿC₂ - n = n(n-3) / 2
Applying the Formula to the Hexagon
For a hexagon (n = 6), let's apply this formula:
Number of diagonals = ⁶C₂ - 6 = (6 x 5) / (2 x 1) - 6 = 15 - 6 = 9
This confirms our earlier result: a hexagon has 9 diagonals.
Method 3: Systematic Approach and Pattern Recognition
Let's explore a more systematic approach. Consider the following:
- Triangle (3 sides): 0 diagonals
- Square (4 sides): 2 diagonals
- Pentagon (5 sides): 5 diagonals
- Hexagon (6 sides): 9 diagonals
- Heptagon (7 sides): 14 diagonals
- Octagon (8 sides): 20 diagonals
Notice a pattern emerging? The difference between consecutive numbers of diagonals increases by 1 each time (0, 2, 5, 9, 14, 20... the differences are 2, 3, 4, 5, 6...). This pattern can be represented by a quadratic function, which can be derived from the combinatorial formula above. This method offers insight into the underlying mathematical relationship between the number of sides and the number of diagonals.
Practical Applications and Further Exploration
Understanding the number of diagonals in polygons has practical applications in various fields:
-
Computer Graphics: Algorithms for drawing and manipulating polygons in computer graphics often rely on understanding the connectivity between vertices. Knowing the number of diagonals is essential for efficient rendering and manipulation.
-
Network Topology: In network design, understanding polygon properties can help in optimizing network connectivity and minimizing redundancy.
-
Structural Engineering: Analyzing the strength and stability of structures often involves understanding the connections between different components, which can be modeled using polygons and their diagonals.
-
Game Development: Game developers use geometric principles to create realistic environments and game mechanics. Calculating diagonals helps in determining distances and creating accurate representations of shapes and structures.
Conclusion
The question of how many diagonals a hexagon has is more than a simple geometry problem. It provides a valuable opportunity to explore different mathematical concepts, including combinatorics and pattern recognition. Understanding these methods enables us to calculate the number of diagonals for any polygon and appreciate the underlying mathematical principles that govern geometric shapes. Moreover, the application of this knowledge extends far beyond the classroom, impacting various fields that depend on geometric calculations and spatial reasoning. Whether you prefer visual counting, combinatorial formulas, or pattern recognition, understanding the solution enriches your mathematical intuition and problem-solving skills.
Latest Posts
Latest Posts
-
How Many Feet Is 34 Inches
Mar 30, 2025
-
Molecular Mass Of Ca3 Po4 2
Mar 30, 2025
-
Why Do We Resemble Our Parents
Mar 30, 2025
-
What Is The Factor Of 102
Mar 30, 2025
-
What Are All Multiples Of 3
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about How Many Diagonals Does A Hexagon Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
