What Is The Factor Of 102
Juapaving
Mar 30, 2025 · 6 min read
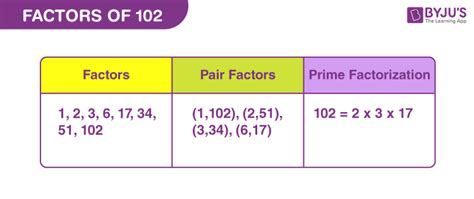
Table of Contents
What are the Factors of 102? A Deep Dive into Number Theory
Finding the factors of a number might seem like a simple arithmetic task, but it opens the door to a fascinating world of number theory. Understanding factors is fundamental to many mathematical concepts, from simplifying fractions to solving complex equations. This article will explore the factors of 102 in detail, explaining the process of finding them, delving into related number theory concepts, and showing how this seemingly simple exercise connects to broader mathematical ideas.
Understanding Factors
Before we delve into the specific factors of 102, let's define what a factor is. A factor (or divisor) of a number is a whole number that divides the number exactly without leaving a remainder. In simpler terms, it's a number that you can multiply by another whole number to get the original number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because:
- 1 x 12 = 12
- 2 x 6 = 12
- 3 x 4 = 12
Finding all the factors of a number is a crucial step in various mathematical operations, including:
- Simplifying fractions: Identifying common factors allows you to reduce fractions to their simplest form.
- Finding the greatest common divisor (GCD): The GCD of two numbers is the largest number that divides both without leaving a remainder. Understanding factors is essential to find the GCD.
- Prime factorization: Breaking down a number into its prime factors (factors that are only divisible by 1 and themselves) is a cornerstone of number theory.
Finding the Factors of 102: A Step-by-Step Approach
Now, let's systematically find all the factors of 102. We'll employ a methodical approach to ensure we don't miss any.
1. Start with 1 and the number itself: Every number has 1 and itself as factors. Therefore, 1 and 102 are factors of 102.
2. Check for divisibility by 2: Since 102 is an even number (ends in 2), it's divisible by 2. 102 / 2 = 51. So, 2 and 51 are factors.
3. Check for divisibility by 3: The divisibility rule for 3 states that a number is divisible by 3 if the sum of its digits is divisible by 3. The sum of the digits of 102 (1 + 0 + 2 = 3) is divisible by 3, confirming that 102 is divisible by 3. 102 / 3 = 34. Thus, 3 and 34 are factors.
4. Check for divisibility by other prime numbers: We continue checking for divisibility by prime numbers, which are numbers greater than 1 that are only divisible by 1 and themselves. The next prime number is 6. 102/6 = 17 so 6 and 17 are factors. We've already checked for divisibility by 2, 3, and 6, and we've also established that 17 is a factor. We can stop checking at this point, since 17 is a prime number and the next prime would be larger than the square root of 102 (approximately 10.1), and any factor larger than this would have its pairing factor smaller than 10.1.
5. Listing all factors: Combining all the factors we've found, the factors of 102 are 1, 2, 3, 6, 17, 34, 51, and 102.
Prime Factorization of 102
Prime factorization is the process of expressing a number as a product of its prime factors. This is a fundamental concept in number theory and has many applications in cryptography and other fields. Let's find the prime factorization of 102.
We already know that 102 = 2 x 51. And 51 = 3 x 17. Therefore, the prime factorization of 102 is 2 x 3 x 17. This means that 2, 3, and 17 are the prime factors of 102. All other factors are combinations of these prime factors.
Connecting Factors to Other Mathematical Concepts
The concept of factors extends far beyond simply listing divisors. It's intricately linked to several other important mathematical concepts:
Greatest Common Divisor (GCD)
The GCD of two or more numbers is the largest number that divides all of them without leaving a remainder. For example, let's find the GCD of 102 and 136.
- Factors of 102: 1, 2, 3, 6, 17, 34, 51, 102
- Factors of 136: 1, 2, 4, 8, 17, 34, 68, 136
The common factors of 102 and 136 are 1, 2, 17, and 34. The greatest of these is 34, so the GCD(102, 136) = 34.
Least Common Multiple (LCM)
The LCM of two or more numbers is the smallest number that is a multiple of all of them. To find the LCM, we can use the prime factorization of the numbers. Let's find the LCM of 102 and 136.
- Prime factorization of 102: 2 x 3 x 17
- Prime factorization of 136: 2³ x 17
To find the LCM, we take the highest power of each prime factor present in either number: 2³ x 3 x 17 = 204. Therefore, LCM(102, 136) = 204.
Euclidean Algorithm
The Euclidean algorithm is an efficient method for computing the GCD of two integers. It's based on the principle that the GCD of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCD.
Let's use the Euclidean algorithm to find the GCD of 102 and 136:
- 136 = 102 x 1 + 34
- 102 = 34 x 3 + 0
The remainder is 0, so the GCD is the last non-zero remainder, which is 34.
Applications of Factors and Number Theory
The concepts discussed above, seemingly abstract, have practical applications in various fields:
- Cryptography: Prime factorization is crucial in many encryption algorithms. The difficulty of factoring large numbers into their prime components forms the basis of the security of these systems.
- Computer Science: Number theory plays a significant role in algorithm design and optimization. Understanding factors helps in developing efficient algorithms for various computational tasks.
- Music Theory: Number theory concepts, including factors and ratios, are used to understand musical intervals and harmony.
- Engineering: Factorization and other number theory principles are applied in various engineering disciplines, such as signal processing and coding theory.
Conclusion: The Significance of Understanding Factors
Understanding factors, prime factorization, GCD, and LCM is not just about rote memorization of mathematical procedures. It's about grasping fundamental concepts that underpin more advanced mathematical ideas and have practical applications in diverse fields. The simple act of finding the factors of 102, as we've done in this article, serves as a gateway to a rich and fascinating world of number theory, revealing the beauty and elegance of mathematical relationships. The seemingly simple question, "What are the factors of 102?" unlocks a deeper understanding of the interconnectedness of mathematical concepts and their impact on various aspects of our world.
Latest Posts
Latest Posts
-
Is 35 A Multiple Of 6
Apr 01, 2025
-
Exponents Worksheets Pdf With Answers 7th
Apr 01, 2025
-
Is Chlorine A Pure Substance Or Mixture
Apr 01, 2025
-
How Do You Write 19 In Roman Numerals
Apr 01, 2025
-
Why Is It Warmer When It Snows
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Factor Of 102 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
