How Many Degrees Is In A Rectangle
Juapaving
Mar 21, 2025 · 5 min read
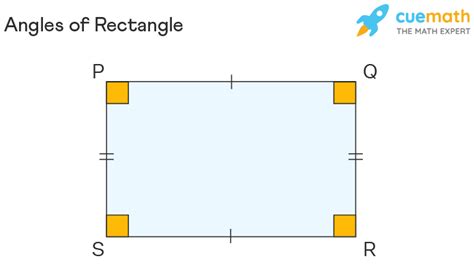
Table of Contents
How Many Degrees are in a Rectangle? A Comprehensive Exploration
The question, "How many degrees are in a rectangle?" seems deceptively simple. While the immediate answer is a straightforward 360°, a deeper dive reveals a wealth of geometric principles and related concepts that are crucial for understanding the properties of rectangles and polygons in general. This article will not only answer the core question but also explore the underlying mathematical reasoning, relevant theorems, and practical applications.
Understanding Angles and Polygons
Before diving into rectangles, let's establish a foundation in basic geometry. Angles are measured in degrees, with a full rotation representing 360°. Polygons are closed shapes with straight sides. The sum of the interior angles of any polygon is determined by its number of sides (n). The formula for calculating this sum is (n-2) * 180°.
The Case of Quadrilaterals
A quadrilateral is a polygon with four sides. Rectangles are a specific type of quadrilateral. Using the formula (n-2) * 180°, we can determine that the sum of the interior angles of any quadrilateral is (4-2) * 180° = 360°. This directly answers our initial question regarding rectangles: a rectangle, being a quadrilateral, has a total of 360° in its interior angles.
Defining a Rectangle
A rectangle is a special type of quadrilateral defined by two key properties:
- All four angles are right angles (90° each). This is the defining characteristic that distinguishes rectangles from other quadrilaterals.
- Opposite sides are parallel and equal in length. This ensures the rectangle's shape is consistent and symmetrical.
These properties are interconnected and interdependent. The fact that opposite sides are parallel and equal directly implies the existence of four 90° angles. Conversely, the presence of four 90° angles guarantees the parallelism and equality of opposite sides.
Theorems and Properties
Several theorems underpin the properties of rectangles:
-
The Pythagorean Theorem: While not directly defining a rectangle, the Pythagorean theorem (a² + b² = c²) is crucial in calculating the diagonal length of a rectangle, given the lengths of its sides (a and b). The diagonal (c) forms a right-angled triangle with two adjacent sides.
-
Parallel Postulate: This fundamental postulate in Euclidean geometry states that given a line and a point not on the line, there is exactly one line through the point that is parallel to the given line. This postulate is essential in understanding the parallel sides of a rectangle.
-
Angle Sum Property of Quadrilaterals: As mentioned earlier, this property guarantees that the sum of interior angles in any quadrilateral, including a rectangle, is 360°.
Beyond the 360° Sum: Exploring Rectangles Further
While the total sum of interior angles is 360°, examining the individual angles provides further insights into the nature of rectangles. The fact that each angle is exactly 90° dictates many other geometric properties:
-
Symmetry: Rectangles possess both rotational and reflectional symmetry. A 180° rotation about the center point keeps the rectangle unchanged. Reflection across either axis of symmetry also results in the same shape.
-
Diagonals: The diagonals of a rectangle bisect each other (they cut each other in half), creating four congruent triangles within the rectangle. Each triangle is a right-angled triangle, with the diagonal as the hypotenuse.
-
Area and Perimeter: The area of a rectangle is simply the product of its length and width (A = l*w). The perimeter is twice the sum of its length and width (P = 2(l+w)). These formulas are easily derived from the rectangular shape and its properties.
-
Special Cases: Squares are a special case of rectangles where all four sides are equal in length. This adds further symmetry and properties. The diagonals of a square are not only equal but also perpendicular bisectors of each other.
Real-World Applications of Rectangular Geometry
Rectangles are ubiquitous in our environment and hold significant importance in many fields:
-
Architecture and Construction: Buildings, rooms, windows, and doors are typically rectangular, simplifying design, construction, and material estimation.
-
Engineering: Rectangular shapes are frequently used in engineering designs for their structural stability and ease of calculation. From bridges to computer chips, rectangles find practical applications.
-
Art and Design: Rectangles provide a foundational structure in art and graphic design, facilitating visual balance and composition.
-
Everyday Objects: Many everyday items, from books and screens to furniture and packaging, are designed with rectangular shapes.
Misconceptions and Clarifications
It's essential to clarify some potential misconceptions regarding rectangles and their angles:
-
Non-Euclidean Geometry: In non-Euclidean geometries, the sum of interior angles of a quadrilateral is not necessarily 360°. These geometries explore alternative systems of axioms and lead to different results. However, the discussion here is solely focused on Euclidean geometry.
-
Distorted Rectangles: A distorted rectangle might appear visually non-rectangular due to perspective or viewing angle, but its underlying properties remain consistent, including the 360° sum of interior angles. The angles themselves might appear skewed but would still add up to 360° in the ideal geometrical sense.
Conclusion: The Significance of 360° in Rectangular Geometry
The simple answer – 360 degrees – to the question of how many degrees are in a rectangle masks a rich mathematical underpinning. The 360° sum of interior angles, combined with the right angles defining a rectangle, leads to a plethora of geometric properties, theorems, and practical applications. Understanding these concepts is not merely an academic exercise; it's fundamental to a wide range of fields, highlighting the importance of seemingly straightforward geometric principles in our world. The rectangle, with its inherent 360°, serves as a foundational shape in geometry, impacting diverse aspects of our lives from architecture to everyday objects.
Latest Posts
Latest Posts
-
What Are The Factor Of 24
Mar 28, 2025
-
List Three Physical Properties Of Ionic Compounds
Mar 28, 2025
-
Which Of The Following Best Describes An Artery
Mar 28, 2025
-
5 Letter Words With E R In The End
Mar 28, 2025
-
Diagonals Of Rhombus Bisect Vertex Angles
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about How Many Degrees Is In A Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
