Diagonals Of Rhombus Bisect Vertex Angles
Juapaving
Mar 28, 2025 · 6 min read
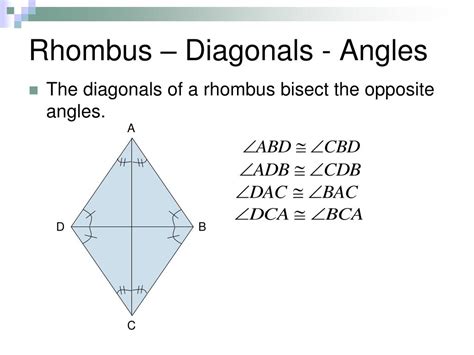
Table of Contents
Diagonals of a Rhombus Bisect Vertex Angles: A Comprehensive Exploration
The rhombus, a captivating quadrilateral with all sides equal, holds a unique geometric property: its diagonals bisect the vertex angles. This seemingly simple statement underpins a wealth of geometric relationships and applications, extending far beyond basic geometry. This article delves deep into this fundamental property, exploring its proof, implications, and practical applications. We’ll examine various approaches to proving this theorem, discuss its connection to other geometric concepts, and showcase its use in problem-solving.
Understanding the Rhombus and its Diagonals
Before embarking on a rigorous proof, let's establish a clear understanding of the rhombus and its diagonals. A rhombus is defined as a quadrilateral with four congruent sides. This inherent symmetry leads to several crucial properties, including:
- Opposite sides are parallel: This makes a rhombus a special case of a parallelogram.
- Opposite angles are equal: This further emphasizes the symmetrical nature of the shape.
- Consecutive angles are supplementary: The sum of any two consecutive angles equals 180 degrees.
- Diagonals bisect each other: This property is shared with parallelograms in general.
- Diagonals are perpendicular bisectors of each other: This is a unique property of the rhombus (and the square).
The diagonals of a rhombus are line segments connecting opposite vertices. They play a crucial role in defining the rhombus's properties and are pivotal in proving the angle bisector theorem.
Proof 1: Using Congruent Triangles
This proof leverages the power of congruent triangles. By strategically dividing the rhombus using its diagonals, we can create congruent triangles, revealing the angle bisector property.
Steps:
-
Consider a rhombus ABCD: Let AC and BD be the diagonals intersecting at point O.
-
Form Triangles: The diagonals divide the rhombus into four triangles: ΔAOB, ΔBOC, ΔCOD, and ΔDOA.
-
Prove Congruence: Since the rhombus has equal sides (AB = BC = CD = DA), and the diagonals bisect each other (AO = OC, BO = OD), we can utilize the Side-Side-Side (SSS) congruence theorem to prove that ΔAOB ≅ ΔCOB ≅ ΔCOD ≅ ΔDOA. This is because AO = OC, BO = OD, and AB = BC = CD = DA.
-
Angle Congruence: Due to the congruence of the triangles, their corresponding angles are equal. This means ∠BAO = ∠CAO and ∠ABO = ∠CBO. Similarly, ∠CBO = ∠DBO and ∠DCO = ∠ACO.
-
Conclusion: Since ∠BAO = ∠CAO and ∠ABO = ∠CBO, the diagonals AC and BD bisect ∠A and ∠B respectively. The same logic applies to angles C and D, proving that the diagonals of a rhombus bisect the vertex angles.
Proof 2: Using Properties of Parallelograms
This proof takes a slightly different approach, starting with the properties of parallelograms and then focusing on the rhombus's unique characteristics.
Steps:
-
Rhombus as a Parallelogram: A rhombus is a parallelogram, so its opposite sides are parallel (AB || DC and AD || BC).
-
Alternate Interior Angles: Because of the parallel lines, alternate interior angles formed by the diagonals are equal. For instance, ∠BAC = ∠DCA and ∠ABD = ∠BDC.
-
Isosceles Triangles: Since AB = BC (equal sides of the rhombus), ΔABC is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are equal, meaning ∠BAC = ∠BCA.
-
Angle Bisector: Combining steps 2 and 3, we have ∠BAC = ∠DCA and ∠BAC = ∠BCA. Therefore, ∠BCA = ∠DCA, indicating that AC bisects ∠C.
-
Generalization: The same logic applies to the other vertices, demonstrating that the diagonals bisect all four vertex angles.
Proof 3: Vector Approach
For those comfortable with vectors, this proof provides an elegant and concise solution.
Steps:
-
Represent Vertices: Let the vertices of the rhombus be represented by vectors a, b, c, and d.
-
Diagonals as Vectors: The diagonals can be represented by vectors c - a and d - b.
-
Midpoint: The midpoint of the diagonals is given by (a + c)/2 and (b + d)/2. Since the diagonals bisect each other, these midpoints are equal.
-
Angle Bisector Condition: Using the dot product of vectors, we can show that the diagonals bisect the angles. The dot product provides a measure of the angle between two vectors. By showing the equality of the dot products of relevant vector pairs, we can prove the angle bisector property. This involves demonstrating the equality of angles formed by the diagonals and the sides of the rhombus.
This vector approach offers a more advanced, yet efficient, method to demonstrate the angle bisector theorem for a rhombus.
Implications and Applications
The theorem that the diagonals of a rhombus bisect its vertex angles has significant implications in various fields:
-
Geometry Problem Solving: This property is invaluable in solving geometric problems involving rhombuses, often simplifying calculations and providing shortcuts. Many problems involving area calculation, angle determination, and side length determination rely on this fundamental theorem.
-
Tessellations and Patterns: The rhombus, with its unique properties including bisected angles, plays a crucial role in creating various tessellations and geometric patterns found in art, architecture, and nature. Understanding angle bisectors aids in the construction and analysis of these complex patterns.
-
Engineering and Design: The symmetrical properties of a rhombus, including the angle bisecting diagonals, find applications in structural engineering, where the symmetrical distribution of forces is critical. This also applies to mechanical design and the creation of various components that benefit from symmetrical stress distribution.
-
Computer Graphics and Game Development: The angle bisector property and the symmetrical nature of the rhombus are used in computer graphics for creating specific shapes, textures, and patterns, streamlining algorithms for generating realistic and efficient representations of objects.
Beyond the Basic: Exploring Related Concepts
The angle bisector property of a rhombus is closely related to several other geometric concepts:
-
Isosceles Triangles: The proof itself relies heavily on the properties of isosceles triangles.
-
Parallelograms: The rhombus is a special case of a parallelogram; understanding parallelogram properties helps to grasp rhombus properties more deeply.
-
Squares: A square is a special type of rhombus (with right angles), making the angle bisector property applicable to squares as well.
-
Kites: While not directly related, the properties of kites share some similarities with rhombuses, particularly concerning diagonals and angle relationships.
Conclusion
The seemingly simple statement that the diagonals of a rhombus bisect the vertex angles underpins a vast array of geometric relationships and practical applications. Through various proofs, from the straightforward use of congruent triangles to the more advanced vector approach, we’ve established the validity of this theorem. Understanding this fundamental property unlocks a deeper appreciation of the rhombus's unique characteristics and expands our problem-solving capabilities in geometry and related fields. Its implications extend beyond the realm of pure mathematics, finding relevance in various practical applications, from tessellations to engineering design. This theorem serves as a cornerstone in the broader study of geometry and underscores the power of seemingly simple geometric truths.
Latest Posts
Latest Posts
-
What Is The Factor Of 71
Mar 31, 2025
-
Force Per Unit Area Is Termed
Mar 31, 2025
-
Consecutive Angles Of A Parallelogram Are Supplementary
Mar 31, 2025
-
What Are 5 Examples Of Chemical Weathering
Mar 31, 2025
-
5 Letter Words Starting With H A I
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Diagonals Of Rhombus Bisect Vertex Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
