Highest Common Factor Of 36 And 84
Juapaving
Mar 28, 2025 · 5 min read
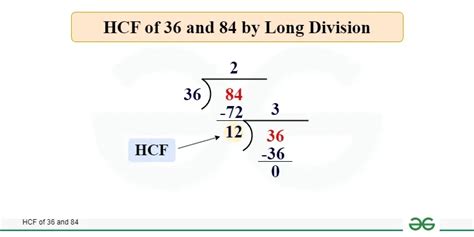
Table of Contents
Finding the Highest Common Factor (HCF) of 36 and 84: A Comprehensive Guide
The highest common factor (HCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. Finding the HCF is a fundamental concept in number theory with applications in various fields, from simplifying fractions to solving complex mathematical problems. This article delves deep into the methods of calculating the HCF of 36 and 84, exploring multiple approaches and illustrating the underlying mathematical principles. We'll move beyond just finding the answer and delve into the 'why' behind each method, equipping you with a thorough understanding of this crucial mathematical operation.
Understanding the Concept of Highest Common Factor
Before we jump into calculating the HCF of 36 and 84, let's solidify our understanding of the concept. The HCF represents the largest common factor shared by two or more numbers. A factor is a number that divides another number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
Finding the HCF involves identifying all the factors of each number and then selecting the largest factor that is common to both. This process can become cumbersome with larger numbers, hence the need for efficient methods, which we'll explore in detail.
Method 1: Prime Factorization Method
The prime factorization method is a systematic way to find the HCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 36 and 84:
1. Prime Factorization of 36:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²
2. Prime Factorization of 84:
84 = 2 x 42 = 2 x 2 x 21 = 2 x 2 x 3 x 7 = 2² x 3 x 7
3. Identifying Common Prime Factors:
Now, we compare the prime factorizations of 36 and 84. The common prime factors are 2² and 3.
4. Calculating the HCF:
To find the HCF, we multiply the common prime factors raised to their lowest powers:
HCF(36, 84) = 2² x 3 = 4 x 3 = 12
Therefore, the highest common factor of 36 and 84 is 12.
Method 2: Euclidean Algorithm
The Euclidean algorithm provides a more efficient method for finding the HCF, especially when dealing with larger numbers. This algorithm is based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Let's apply the Euclidean algorithm to 36 and 84:
1. Start with the larger number (84) and the smaller number (36):
84 = 2 x 36 + 12
2. Replace the larger number (84) with the remainder (12) and repeat the process:
36 = 3 x 12 + 0
3. Since the remainder is 0, the HCF is the last non-zero remainder, which is 12.
Therefore, the highest common factor of 36 and 84 using the Euclidean algorithm is 12. This method is remarkably efficient, especially for larger numbers where prime factorization can become quite tedious.
Method 3: Listing Factors Method
This method, although less efficient for larger numbers, is conceptually simple. We list all the factors of both numbers and identify the largest common factor.
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Comparing the lists, we see that the common factors are 1, 2, 3, 4, 6, and 12. The largest of these is 12, confirming our previous results.
Applications of Finding the HCF
The concept of the highest common factor extends far beyond simple mathematical exercises. It has practical applications in various fields:
1. Simplifying Fractions:
The HCF is crucial for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their HCF. For example, the fraction 36/84 can be simplified by dividing both 36 and 84 by their HCF, 12, resulting in the simplified fraction 3/7.
2. Solving Word Problems:
Many word problems involving division and equal sharing utilize the concept of the HCF. For instance, imagine you have 36 apples and 84 oranges, and you want to divide them into identical bags with the maximum number of fruits in each bag, without any leftover fruit. The HCF(36, 84) = 12 determines that you can create 12 bags, each containing 3 apples and 7 oranges.
3. Geometry and Measurement:
The HCF finds application in geometrical problems involving the division of lengths or areas. Imagine you need to cut a piece of wood of length 36 cm and another of length 84 cm into smaller identical pieces of the maximum possible length without any waste. The solution, again, lies in the HCF(36, 84) = 12 cm, signifying that the maximum length for each piece is 12 cm.
4. Cryptography and Number Theory:
The HCF plays a significant role in more advanced mathematical areas like cryptography and number theory. Algorithms used in encryption and decryption often rely on finding the HCF of large numbers.
Conclusion: Mastering the HCF
Understanding and calculating the highest common factor is a cornerstone of mathematical proficiency. Whether you're simplifying fractions, solving word problems, or exploring more advanced mathematical concepts, the ability to efficiently determine the HCF is essential. This article has explored three distinct methods – prime factorization, the Euclidean algorithm, and listing factors – providing a comprehensive understanding of this fundamental concept. By grasping these methods and their underlying principles, you'll be equipped to tackle a wide range of mathematical problems confidently and effectively. Remember that the choice of method often depends on the size of the numbers involved; the Euclidean algorithm tends to be the most efficient for larger numbers. Consistent practice with various examples will solidify your understanding and enhance your problem-solving skills. So, continue exploring the fascinating world of numbers and their intricate relationships!
Latest Posts
Latest Posts
-
How To Find Reciprocal Of A Mixed Number
Mar 31, 2025
-
Which Of The Following Is Considered A Micronutrient
Mar 31, 2025
-
How Many Inches Is 2 Meters
Mar 31, 2025
-
What Medical Problem Afflicts Mrs Mallard
Mar 31, 2025
-
2 Over 5 As A Percent
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Highest Common Factor Of 36 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
