Given A 120 Degree Angle Construct A 0 Degree Angle
Juapaving
Apr 05, 2025 · 5 min read
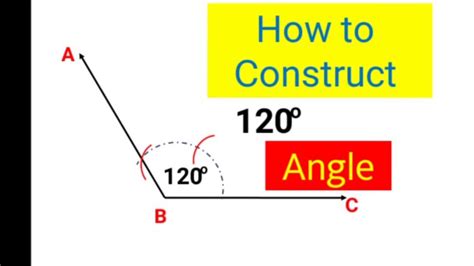
Table of Contents
Constructing a 0° Angle from a 120° Angle: A Comprehensive Guide
Constructing a 0° angle, or a straight line, from a given 120° angle might seem deceptively simple. After all, a straight line is fundamental in geometry. However, the process involves understanding fundamental geometric principles and applying them accurately. This comprehensive guide will explore various methods to achieve this construction, focusing on accuracy and clarity, suitable for both beginners and those seeking a deeper understanding of geometric principles.
Understanding the Fundamentals: Angles and Lines
Before diving into the construction process, let's revisit some basic geometric concepts:
Angles:
An angle is formed by two rays sharing a common endpoint, called the vertex. Angles are measured in degrees, with a 0° angle representing two overlapping rays forming a straight line, and a 180° angle representing a straight line. A 120° angle is an obtuse angle, meaning it's greater than 90° but less than 180°.
Lines:
A line extends infinitely in both directions. A line segment is a portion of a line with two endpoints. A ray has one endpoint and extends infinitely in one direction. The construction of a 0° angle ultimately involves creating a straight line.
Geometric Tools:
The constructions will utilize standard geometric tools:
- Ruler: For drawing straight lines and measuring lengths.
- Compass: For creating circles and arcs of specific radii.
- Protractor (Optional): While not strictly necessary for the construction itself, a protractor can be used for verification.
Method 1: Using the Compass and Ruler to Bisect the Angle
This method leverages the power of angle bisection to achieve the desired 0° angle.
Steps:
-
Draw the 120° Angle: Start by drawing the given 120° angle. Label the vertex as 'A' and the two rays as 'AB' and 'AC'.
-
Draw Arcs: Place the compass point at vertex A. Draw an arc that intersects ray AB at point 'D' and ray AC at point 'E'. Maintain the same compass radius.
-
Intersect the Arcs: Without changing the compass radius, place the compass point at D. Draw an arc. Repeat this process, placing the compass point at E and drawing another arc that intersects the arc from D. Label the intersection point as 'F'.
-
Draw the Bisector: Draw a line segment from vertex A through point F. This line segment bisects the 120° angle, creating two 60° angles.
-
Bisect Again: Repeat steps 2-4, but this time using the 60° angle created. This bisects the 60° angle into two 30° angles.
-
Bisect one last time: Repeat steps 2-4 one last time on one of the 30° angles. This bisects the 30° angle into two 15° angles. The line created in this step will form a 15° angle with the line segment AF.
-
Creating the 0° Angle (Straight Line): Extend the line segment formed from bisecting the 15 degree angle to create a straight line. This line represents a 0° angle.
Explanation:
By repeatedly bisecting the angle, we systematically reduce its magnitude. Each bisection halves the angle, leading to progressively smaller angles. The final extended line represents the desired 0° angle, or straight line, constructed from the initial 120° angle.
Method 2: Utilizing Supplementary Angles
This method exploits the concept of supplementary angles—two angles that add up to 180°.
Steps:
-
Extend a Ray: Extend one of the rays of the 120° angle (say, ray AB) to create a line.
-
Measure the Supplementary Angle: The angle formed between the extended ray and the other ray (AC) is a supplementary angle to the 120° angle. This supplementary angle measures 180° - 120° = 60°.
-
Construct a 60° Angle: Construct a 60° angle using the compass and ruler. This can be achieved by constructing an equilateral triangle.
-
Combine Angles: Place the 60° angle such that one of its rays aligns with the ray AC. The other ray of the 60° angle will now form a straight line with the extended ray AB, thus creating the 0° angle (straight line).
Explanation:
This method directly uses the relationship between supplementary angles to generate a 180° angle (straight line) and implicitly achieves the 0° angle construction.
Method 3: Using Geometric Transformations (Rotation)
This method employs the concept of rotation in geometry. While more conceptually advanced, it provides a different perspective on the construction.
Steps:
-
Rotate the Angle: Imagine rotating one ray of the 120° angle by 60° around the vertex. This can be visualized, but not easily constructed with only compass and ruler.
-
Align Rays: After the 60° rotation, the two rays would overlap, forming a 0° angle (a straight line). Again, the visualization is more important than precisely constructing a rotation using compass and ruler.
Explanation:
Rotation, as a geometric transformation, provides a different way to think about achieving a straight line from an initial angle. While not directly constructible using only a compass and ruler in this case without additional steps as noted above, the concept serves as a valuable illustration of the underlying principles involved.
Accuracy and Precision
The accuracy of the construction depends on the precision in using the compass and ruler. Small errors in drawing arcs or lines can accumulate, leading to deviations from the ideal 0° angle (straight line). To minimize errors:
- Use Sharp Pencil: A sharp pencil ensures precise marking.
- Draw Light Lines: Light lines allow easy correction of mistakes.
- Check Measurements: Use a protractor (optional) to verify the angles at each stage, especially during bisection.
Conclusion: Multiple Paths to a Straight Line
Constructing a 0° angle (straight line) from a 120° angle involves applying foundational geometric concepts. The methods described above—bisecting the angle, utilizing supplementary angles, and considering rotation—demonstrate different approaches to achieving the same result. Each method offers valuable insight into geometric principles and helps solidify understanding of angles and lines. The choice of method often depends on personal preference and the available tools. Remember that precise use of the compass and ruler is crucial for achieving accurate constructions. This guide provides not only a practical guide but also fosters a deeper understanding of the geometric principles at play. Practicing these constructions will improve your geometric skills and ability to visualize and manipulate spatial relationships.
Latest Posts
Latest Posts
-
Buffer Region On A Titration Curve
Apr 06, 2025
-
What Is The Relationship Between Kinetic And Potential Energy
Apr 06, 2025
-
Conversion Of Mechanical Energy To Electrical Energy
Apr 06, 2025
-
Is A Rectangle A Regular Polygon
Apr 06, 2025
-
5 Letter Words Starting With R I
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Given A 120 Degree Angle Construct A 0 Degree Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
