Least Common Multiple 15 And 25
Juapaving
Apr 03, 2025 · 5 min read
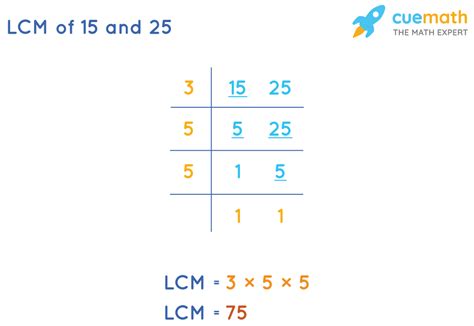
Table of Contents
Finding the Least Common Multiple (LCM) of 15 and 25: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding LCMs is crucial for various applications, from simplifying fractions to solving problems involving cyclical events. This article delves deep into calculating the LCM of 15 and 25, exploring multiple methods and illustrating their practical applications. We'll also examine the broader context of LCMs and their significance in mathematics and beyond.
Understanding Least Common Multiples
Before we jump into finding the LCM of 15 and 25, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors.
For instance, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... Multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples are 6, 12, 18... The smallest of these common multiples is 6; therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
One of the simplest methods for finding the LCM, especially for smaller numbers like 15 and 25, is by listing their multiples. Let's do this:
Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150...
Multiples of 25: 25, 50, 75, 100, 125, 150, 175...
By comparing the lists, we can see that the smallest common multiple is 75. Therefore, the LCM(15, 25) = 75.
This method is effective for smaller numbers but becomes less practical as the numbers get larger. Imagine trying to list multiples for numbers like 147 and 231! That's where more sophisticated methods come into play.
Method 2: Prime Factorization
The prime factorization method is a more robust and efficient way to find the LCM of any two (or more) integers. This method involves breaking down each number into its prime factors – prime numbers that multiply to give the original number.
Prime Factorization of 15:
15 = 3 x 5
Prime Factorization of 25:
25 = 5 x 5 = 5²
Now, to find the LCM, we consider the highest power of each prime factor present in the factorizations:
- The prime factor 3 appears once in the factorization of 15.
- The prime factor 5 appears twice (5²) in the factorization of 25.
Therefore, the LCM is the product of the highest powers of all prime factors involved:
LCM(15, 25) = 3 x 5² = 3 x 25 = 75
This method is far more efficient than listing multiples, particularly when dealing with larger numbers.
Method 3: Using the Formula LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
First, we need to find the GCD of 15 and 25. We can use the Euclidean algorithm for this:
- Divide the larger number (25) by the smaller number (15): 25 ÷ 15 = 1 with a remainder of 10.
- Replace the larger number with the remainder (10) and repeat: 15 ÷ 10 = 1 with a remainder of 5.
- Repeat again: 10 ÷ 5 = 2 with a remainder of 0.
- The last non-zero remainder is the GCD, which is 5. Therefore, GCD(15, 25) = 5.
Now, we can use the formula:
LCM(15, 25) = (15 x 25) / GCD(15, 25) = (375) / 5 = 75
This formula provides a concise and efficient way to calculate the LCM, especially when dealing with numbers that might not have easily identifiable prime factorizations.
Applications of LCM
Understanding and calculating LCMs has numerous applications across various fields:
-
Fraction Arithmetic: Finding the LCM is essential when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator, making the fractions easily comparable and combinable.
-
Scheduling and Cyclical Events: LCMs are used to determine when events with different periodicities will occur simultaneously. For example, if two machines operate on cycles of 15 and 25 minutes, respectively, the LCM (75 minutes) indicates when they will both start their cycles simultaneously.
-
Modular Arithmetic: In modular arithmetic, the LCM plays a crucial role in finding solutions to congruences.
-
Music Theory: LCMs are relevant in music theory for determining harmonic intervals and finding common time signatures.
-
Computer Science: LCMs are used in algorithms related to scheduling, resource allocation and synchronization.
Extending to More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider the highest power of each prime factor present in all factorizations. For the GCD-based formula, you would need to extend the GCD calculation to encompass all the numbers involved, and then apply a generalized formula.
Conclusion: The LCM of 15 and 25 and Beyond
We've explored various methods for finding the least common multiple of 15 and 25, confirming that the LCM(15, 25) = 75. We've seen that the prime factorization method offers a particularly robust and efficient approach, especially when dealing with larger numbers or multiple numbers. Understanding LCMs is not just about theoretical mathematics; it's a practical tool with widespread applications in various fields. Mastering the concept of LCM strengthens your mathematical foundation and opens doors to solving a wide range of problems. From simple fraction addition to complex scheduling problems, the LCM remains a fundamental concept with enduring relevance. Now you are equipped with the knowledge and different methods to confidently tackle LCM problems of any complexity.
Latest Posts
Latest Posts
-
25 Cm Equals How Many Inches
Apr 04, 2025
-
Whats The Lcm Of 8 And 12
Apr 04, 2025
-
Why India Is Known As Subcontinent
Apr 04, 2025
-
Label The Parts Of A Motor Neuron
Apr 04, 2025
-
What Is Lix In Roman Numerals
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple 15 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
