Find The Prime Factors Of 125
Juapaving
Apr 05, 2025 · 5 min read
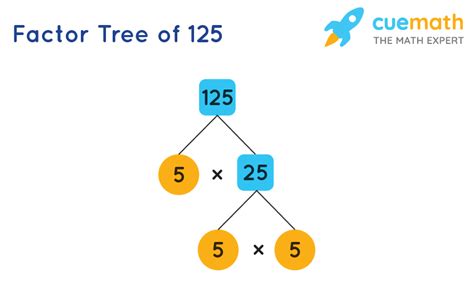
Table of Contents
Finding the Prime Factors of 125: A Deep Dive into Number Theory
Finding the prime factors of a number is a fundamental concept in number theory, crucial for various mathematical applications. This article will explore the process of finding the prime factors of 125, demonstrating the techniques involved and expanding on the broader context of prime factorization. We'll cover different methods, discuss the significance of prime numbers, and touch upon practical applications of prime factorization.
Understanding Prime Numbers and Prime Factorization
Before delving into the prime factorization of 125, let's establish a firm understanding of the key concepts:
Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Prime numbers are the building blocks of all other natural numbers.
Prime Factorization (or Integer Factorization): This is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. Every composite number can be uniquely expressed as a product of prime numbers, a concept known as the Fundamental Theorem of Arithmetic. This unique representation is crucial in various mathematical computations and algorithms.
Methods for Finding the Prime Factors of 125
There are several ways to find the prime factors of 125. We'll explore two common approaches:
Method 1: Repeated Division by Prime Numbers
This method involves systematically dividing the number by the smallest prime number possible, continuing until the quotient becomes 1.
-
Start with the smallest prime number, 2: 125 is not divisible by 2 (it's odd).
-
Move to the next prime number, 3: 125 is not divisible by 3 (the sum of its digits, 1+2+5=8, is not divisible by 3).
-
Move to the next prime number, 5: 125 is divisible by 5 (125 ÷ 5 = 25).
-
Continue with the quotient: Now we consider the quotient, 25. 25 is also divisible by 5 (25 ÷ 5 = 5).
-
Final Prime Factor: The quotient is now 5, which is itself a prime number.
Therefore, the prime factorization of 125 is 5 x 5 x 5, or 5³.
Method 2: Factor Tree
A factor tree is a visual representation of the prime factorization process. It's particularly helpful for larger numbers.
125
/ \
5 25
/ \
5 5
We start by finding any two factors of 125. The most obvious is 5 and 25. We then continue factoring until all the branches end in prime numbers. As we see, the prime factorization is again 5 x 5 x 5 = 5³.
Significance of Prime Factorization
The seemingly simple act of finding prime factors holds profound significance in various areas of mathematics and computer science:
-
Cryptography: Many modern encryption algorithms, such as RSA, rely heavily on the difficulty of factoring large numbers into their prime factors. The security of these systems depends on the computational infeasibility of factoring extremely large semiprime numbers (numbers that are the product of two prime numbers).
-
Number Theory: Prime factorization is fundamental to many theorems and concepts in number theory, including modular arithmetic, Fermat's Little Theorem, and the Chinese Remainder Theorem.
-
Abstract Algebra: Prime factorization plays a critical role in abstract algebra, particularly in the study of rings and ideals.
-
Computer Science: Efficient algorithms for prime factorization are actively researched, with implications for cryptography and other computational problems.
Applications of Prime Factorization Beyond Mathematics
While the core applications reside within mathematical disciplines, the principle of breaking down a complex entity into its fundamental components finds parallels in other fields:
-
Software Engineering: Modular programming, where complex systems are broken down into smaller, more manageable modules, mirrors the concept of prime factorization. Each module is like a prime factor, and their combination builds the complete system.
-
Data Analysis: Analyzing large datasets often involves identifying patterns and breaking down complex relationships into simpler components. This parallels the process of prime factorization, where a large number is decomposed into its prime factors for easier analysis.
Exploring Further: Beyond 125
While we've focused on 125, the techniques demonstrated are applicable to any number. Let's consider some examples to solidify our understanding:
-
Finding the prime factors of 36: The factor tree would show 36 = 2 x 2 x 3 x 3 = 2² x 3².
-
Finding the prime factors of 100: The factor tree reveals 100 = 2 x 2 x 5 x 5 = 2² x 5².
-
Finding the prime factors of 252: Applying the repeated division method or a factor tree yields 252 = 2 x 2 x 3 x 3 x 7 = 2² x 3² x 7.
These examples highlight the versatility and power of prime factorization. No matter how large the number, it can always be broken down into its unique prime components.
Conclusion: The Enduring Importance of Prime Factors
Finding the prime factors of 125, while seemingly a simple task, underscores the fundamental importance of prime numbers and prime factorization in mathematics and beyond. The seemingly straightforward process holds significant implications in cryptography, number theory, and even software engineering. Understanding prime factorization is essential for anyone interested in delving deeper into the fascinating world of numbers and their properties. The unique representation provided by prime factorization is a cornerstone of mathematical understanding, constantly revealing new insights and driving innovation in diverse fields. The power lies not only in the process itself but also in the broader implications it holds for the advancement of mathematical theory and its practical applications.
Latest Posts
Latest Posts
-
Elbow Joint Is An Example Of
Apr 05, 2025
-
Glomerular Filtrate Is Least Likely To Contain
Apr 05, 2025
-
Find The Prime Factorization Of 27
Apr 05, 2025
-
Difference Between Operation And Production Management
Apr 05, 2025
-
Conclusion Of Millikan Oil Drop Experiment
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Find The Prime Factors Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
