Find The Lcm Of 6 And 14
Juapaving
Apr 05, 2025 · 5 min read
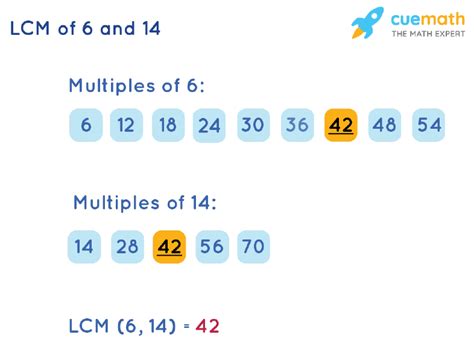
Table of Contents
Finding the LCM of 6 and 14: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with applications across various fields, from scheduling to music theory. This comprehensive guide will delve into the process of finding the LCM of 6 and 14, explaining multiple methods and providing a deeper understanding of the underlying principles. We'll also explore the broader context of LCMs and their significance.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 6 and 14, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the numbers. Think of it as the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... and multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples are 6, 12, 18... The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method for finding the LCM of small numbers like 6 and 14 is by listing their multiples until a common multiple is found.
Steps:
- List multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48...
- List multiples of 14: 14, 28, 42, 56, 70...
- Identify the smallest common multiple: The smallest number that appears in both lists is 42.
Therefore, the LCM of 6 and 14 is 42.
This method is straightforward for small numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Steps:
- Find the prime factorization of 6: 6 = 2 x 3
- Find the prime factorization of 14: 14 = 2 x 7
- Identify the unique prime factors: The unique prime factors are 2, 3, and 7.
- Construct the LCM: Take the highest power of each unique prime factor and multiply them together. In this case, the highest power of 2 is 2<sup>1</sup>, the highest power of 3 is 3<sup>1</sup>, and the highest power of 7 is 7<sup>1</sup>. Therefore, LCM(6, 14) = 2 x 3 x 7 = 42.
Therefore, the LCM of 6 and 14 using prime factorization is 42. This method is generally preferred for larger numbers as it is more systematic and avoids the potentially lengthy process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
Steps:
- Find the GCD of 6 and 14: The factors of 6 are 1, 2, 3, and 6. The factors of 14 are 1, 2, 7, and 14. The greatest common factor is 2. Therefore, GCD(6, 14) = 2.
- Apply the formula: LCM(6, 14) x GCD(6, 14) = 6 x 14
- Solve for LCM: LCM(6, 14) x 2 = 84 LCM(6, 14) = 84 / 2 = 42
Therefore, the LCM of 6 and 14 using the GCD is 42. This method requires understanding how to find the GCD, which can be done using prime factorization or the Euclidean algorithm (explained below).
Method 4: Euclidean Algorithm for GCD
The Euclidean algorithm is an efficient method for finding the GCD of two numbers, especially when dealing with larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Steps:
- Divide the larger number (14) by the smaller number (6): 14 = 2 x 6 + 2
- Replace the larger number with the smaller number (6) and the smaller number with the remainder (2): 6 = 3 x 2 + 0
- The last non-zero remainder is the GCD: The last non-zero remainder is 2, so GCD(6, 14) = 2.
- Use the formula: LCM(6, 14) = (6 x 14) / GCD(6, 14) = (84) / 2 = 42
Therefore, using the Euclidean algorithm to find the GCD and then the LCM, we again arrive at 42. This method is particularly useful for larger numbers where listing multiples or directly finding prime factorization becomes cumbersome.
Applications of LCM
The concept of LCM has numerous applications in various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if two buses arrive at a stop every 6 minutes and 14 minutes respectively, the LCM (42 minutes) tells us when they will both arrive at the stop at the same time.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Music Theory: Determining the least common multiple of different note durations to find the shortest time interval when multiple rhythmic patterns align.
-
Engineering: Synchronization of mechanical systems or processes with varying periodicities.
-
Computer Science: In algorithms and data structures, particularly those related to cyclic processes or periodic tasks.
Conclusion
Finding the LCM of 6 and 14, though seemingly a simple problem, provides a stepping stone to understanding a crucial mathematical concept with significant real-world applications. We have explored multiple methods – listing multiples, prime factorization, using the GCD, and the Euclidean algorithm – each offering a different approach to solving this type of problem. The chosen method depends on the complexity of the numbers involved and the available tools. Mastering the concept of LCM and its various methods is essential for anyone working with numbers and their relationships. Understanding the underlying principles allows for efficient problem-solving and a deeper appreciation of the interconnectedness of mathematical concepts. Remember to choose the method that best suits your needs and the complexity of the numbers involved. The key is to understand the core concept of the least common multiple and the relationship between LCM and GCD.
Latest Posts
Latest Posts
-
Difference Between Quartz And Quartz Glass
Apr 05, 2025
-
Words That Start With A Z
Apr 05, 2025
-
How Much Is 70 Cm In Inches
Apr 05, 2025
-
Benedicts Reagent Is Used To Identify Which Of The Following
Apr 05, 2025
-
What Is A Positively Charged Ion Called
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Find The Lcm Of 6 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
