Find Area Under The Curve Calculator
Juapaving
Mar 30, 2025 · 6 min read
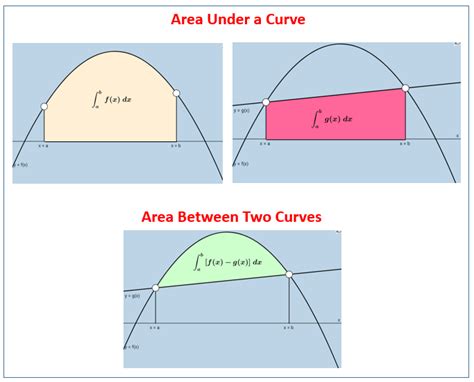
Table of Contents
Find Area Under the Curve Calculator: A Comprehensive Guide
Finding the area under a curve is a fundamental concept in calculus with wide-ranging applications in various fields, from physics and engineering to economics and statistics. Manually calculating this area can be complex and time-consuming, especially for intricate functions. This is where an area under the curve calculator becomes invaluable. This guide will explore the significance of these calculators, delve into different methods for calculating this area, discuss the various types of calculators available, and highlight their practical applications.
What is the Area Under the Curve?
The area under a curve, more formally known as definite integral, represents the area bounded by the curve of a function, the x-axis, and two vertical lines corresponding to specified limits of integration. It essentially quantifies the accumulated value of the function over a given interval. Imagine you have a velocity-time graph. The area under the curve represents the total distance traveled. Similarly, in economics, the area under a demand curve represents the total consumer surplus.
Importance of Calculating the Area Under the Curve
Calculating the area under the curve is crucial for numerous reasons:
-
Solving real-world problems: Many real-world phenomena can be modeled using curves, and the area under the curve provides meaningful insights. Examples include calculating work done by a variable force, determining the total distance traveled with varying velocity, or estimating the total revenue generated from a varying demand curve.
-
Evaluating integrals: The area under the curve is the graphical representation of a definite integral. Understanding this relationship is vital for mastering integral calculus.
-
Statistical analysis: In statistics, the area under the curve of a probability density function represents the probability of a random variable falling within a particular range. This is fundamental in hypothesis testing and confidence interval estimation.
-
Engineering and physics: Calculating areas under curves is essential in fields like fluid mechanics, thermodynamics, and structural analysis.
Methods for Calculating the Area Under the Curve
Several methods exist for finding the area under the curve, each with its strengths and limitations:
1. Analytical Methods (Using Calculus):
This approach involves using integration techniques to find the exact area. It requires knowledge of calculus and can be challenging for complex functions. The process typically involves:
- Finding the indefinite integral: This is the antiderivative of the function.
- Evaluating the definite integral: This involves substituting the upper and lower limits of integration into the indefinite integral and subtracting the results.
Example: Let's say we want to find the area under the curve y = x² from x = 0 to x = 2.
- Find the indefinite integral: ∫x² dx = (1/3)x³ + C (where C is the constant of integration)
- Evaluate the definite integral: [(1/3)(2)³ + C] - [(1/3)(0)³ + C] = 8/3
Therefore, the area under the curve is 8/3 square units.
2. Numerical Methods (Approximation Techniques):
When analytical methods are impractical, numerical methods provide approximate solutions. These methods are particularly useful for functions that are difficult or impossible to integrate analytically. Common numerical methods include:
-
Riemann Sums: This method approximates the area using rectangles. The accuracy increases with the number of rectangles used. There are three main types: left Riemann sum, right Riemann sum, and midpoint Riemann sum.
-
Trapezoidal Rule: This method approximates the area using trapezoids, which generally provides a more accurate approximation than Riemann sums.
-
Simpson's Rule: This method approximates the area using parabolas, offering even greater accuracy than the trapezoidal rule, especially for smoother curves.
3. Using an Area Under the Curve Calculator
Area under the curve calculators utilize these numerical methods (and sometimes symbolic integration for simpler functions) to provide a quick and accurate solution. They eliminate the need for manual calculations, saving time and effort.
Types of Area Under the Curve Calculators
Several types of calculators cater to different needs and levels of expertise:
-
Simple Online Calculators: These calculators usually require inputting the function, the lower and upper limits of integration, and sometimes the number of subdivisions (for numerical methods). They provide a quick result and are suitable for basic calculations.
-
Advanced Online Calculators: These calculators often offer more features, such as plotting the function, visualizing the area being calculated, and selecting different numerical integration methods. They are useful for understanding the process and comparing results from different methods.
-
Software Packages: Many mathematical software packages, such as MATLAB, Mathematica, and Maple, include sophisticated functions for calculating definite integrals and visualizing the area under the curve. These tools are powerful but require some learning curve.
-
Graphing Calculators: Some graphing calculators have built-in functions for numerical integration, allowing for quick calculations and visualization on the device itself.
Applications of Area Under the Curve Calculators
The applications are vast and span numerous disciplines:
-
Physics: Calculating work done by a variable force, determining the distance traveled with non-constant velocity, finding the center of mass of an object.
-
Engineering: Determining the volume of irregularly shaped objects, analyzing stress and strain in materials, calculating fluid flow.
-
Economics: Calculating consumer surplus and producer surplus, analyzing market equilibrium, modeling economic growth.
-
Statistics: Finding probabilities associated with probability density functions, calculating confidence intervals, performing hypothesis tests.
-
Biology: Modeling population growth, analyzing enzyme kinetics, studying drug absorption and elimination.
-
Computer Science: Approximating the value of definite integrals in simulations and algorithms.
Choosing the Right Area Under the Curve Calculator
The best calculator depends on your needs:
-
Simplicity vs. Advanced Features: If you need a quick calculation for a simple function, a basic online calculator will suffice. If you require more advanced features like visualization or different numerical methods, an advanced calculator or software package is more suitable.
-
Accuracy Requirements: Numerical methods provide approximations. The accuracy depends on the method used and the number of subdivisions. For high accuracy, consider using more advanced methods and a larger number of subdivisions.
-
Ease of Use: Choose a calculator with a user-friendly interface, clear instructions, and good documentation.
-
Cost: Online calculators are generally free, while software packages can be expensive.
Conclusion
Calculating the area under the curve is a powerful technique with applications across diverse fields. While analytical methods offer exact solutions when feasible, numerical methods and area under the curve calculators provide practical and efficient solutions for complex functions. Understanding the different methods and choosing the right tool are crucial for successfully applying this fundamental concept. The availability of user-friendly online calculators and powerful software packages makes this essential mathematical operation accessible to a wide range of users, simplifying complex problems and enabling deeper insights into various phenomena. By leveraging these tools effectively, professionals and students alike can unlock the power of integral calculus and its applications in their respective fields.
Latest Posts
Latest Posts
-
What Is The Function Of The Collecting Duct
Apr 01, 2025
-
A Rectangle Is A Square Always Sometimes Never
Apr 01, 2025
-
What Are The First 5 Multiples Of 2
Apr 01, 2025
-
What Is The Numeral For 42
Apr 01, 2025
-
Butter Melting Is A Physical Change
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Find Area Under The Curve Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
