A Rectangle Is A Square Always Sometimes Never
Juapaving
Apr 01, 2025 · 5 min read
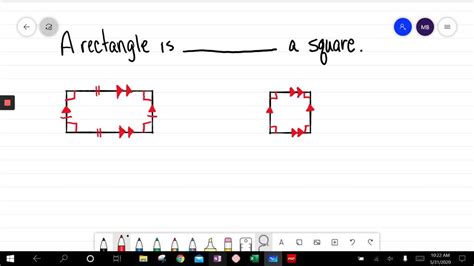
Table of Contents
A Rectangle is a Square: Always, Sometimes, or Never?
The relationship between rectangles and squares is a fundamental concept in geometry that often causes confusion. Many students struggle to differentiate between the two, leading to misconceptions about their properties. This article aims to clarify the relationship between rectangles and squares, definitively answering the question: is a rectangle always, sometimes, or never a square? We'll explore the defining characteristics of each shape, delve into their similarities and differences, and provide clear examples to solidify your understanding.
Understanding Rectangles
A rectangle is a quadrilateral, meaning it's a two-dimensional shape with four sides. However, rectangles possess specific properties that distinguish them from other quadrilaterals:
- Four right angles: Each of the four interior angles measures exactly 90 degrees. This is a crucial defining characteristic.
- Opposite sides are equal and parallel: The lengths of opposite sides are equal, and these sides run parallel to each other.
Importantly, the lengths of adjacent sides in a rectangle do not have to be equal. This is where the distinction from a square becomes clear.
Understanding Squares
A square is also a quadrilateral, inheriting all the properties of a rectangle. However, squares have an additional defining characteristic that elevates them above a simple rectangle:
- All sides are equal: All four sides of a square have the same length.
This equality of sides is the key difference between squares and rectangles.
The Crucial Difference: Side Lengths
The core distinction between rectangles and squares lies in the lengths of their sides. A rectangle only requires opposite sides to be equal and all angles to be right angles. A square, on the other hand, demands all four sides to be equal in length, in addition to the right angles.
Think of it this way: a square is a special type of rectangle, but not all rectangles are squares. A square satisfies all the conditions of a rectangle, but a rectangle does not necessarily satisfy all the conditions of a square.
Visualizing the Relationship
Imagine a rectangle drawn on a piece of paper. If you gradually increase the length of one pair of opposite sides, keeping the right angles intact, you're still working with a rectangle. The shape evolves, becoming longer and thinner, but remains a rectangle. However, if you adjust the lengths of all sides so that they become equal, then – and only then – does the rectangle transform into a square.
Is a Rectangle Always a Square?
No, a rectangle is never always a square. As explained earlier, the defining characteristic of a square (equal side lengths) is not a requirement for a rectangle. Countless examples of rectangles exist where the adjacent sides have different lengths. A standard sheet of paper, a rectangular window, a playing card – these are all rectangles that are demonstrably not squares.
Is a Rectangle Sometimes a Square?
Yes, a rectangle is sometimes a square. This occurs when the lengths of all four sides of the rectangle become equal. In this specific case, the rectangle fulfills all the requirements to also be classified as a square. It inherits all the properties of a rectangle and satisfies the additional condition of equal side lengths.
Is a Rectangle Never a Square?
No, a rectangle is never never a square. The possibility that a rectangle can be a square exists. This happens when the conditions of equal side lengths are met. It's more accurate to say that a rectangle is a square only under a specific condition: when all sides are of equal length.
Real-World Examples
Let's solidify our understanding with real-world examples:
- Rectangles that are NOT squares: A television screen, a door, a book, a field. These objects are typically rectangular but have different side lengths.
- Rectangles that ARE squares: A perfectly square tile, a square piece of artwork, a square window pane. These objects fulfill the requirements of both a rectangle and a square.
Common Mistakes and Misconceptions
A common misconception stems from focusing solely on the right angles. Students might incorrectly think that any four-sided shape with right angles is a square. It's crucial to remember that equal side lengths are the key differentiator between a rectangle and a square.
Another potential pitfall is the assumption that the term "rectangle" excludes squares. It's important to reiterate that squares are a subset of rectangles. This is a hierarchical relationship, with squares being a more specific type of rectangle.
Applying the Concepts: Problem Solving
Let's apply our understanding to a couple of problems:
Problem 1: A quadrilateral has four right angles and two pairs of equal sides. Is it always a square?
Solution: No. This description matches the definition of a rectangle. It could be a square (if all sides are equal), but it could also be a rectangle with unequal adjacent sides.
Problem 2: A quadrilateral has all sides equal and four right angles. What is it?
Solution: This is a square. It satisfies both the definition of a rectangle (four right angles, opposite sides equal) and the additional requirement of a square (all sides equal).
Conclusion: The Definitive Answer
A rectangle is sometimes a square. It is never always a square because the condition of equal side lengths isn't inherent to all rectangles. And it's never never a square because the possibility of a rectangle being a square exists when its sides are equal. The relationship between rectangles and squares is a crucial concept in geometry; understanding their similarities and differences is key to mastering geometric principles. By carefully considering the defining characteristics of each shape, we can accurately classify and analyze different two-dimensional figures. This knowledge is not just beneficial for academic purposes; it finds applications in various fields, from architecture and engineering to design and computer graphics. The ability to discern between rectangles and squares allows for precise calculations, efficient designs, and accurate representations of the physical world.
Latest Posts
Latest Posts
-
Ability To Run Multiple Applications Simultaneously
Apr 02, 2025
-
What Are The Vertical Rows On The Periodic Table Called
Apr 02, 2025
-
What Do You Call The Place Where An Organism Lives
Apr 02, 2025
-
What Are The Common Multiples Of 6 And 9
Apr 02, 2025
-
Are Angiosperms Gametophyte Or Sporophyte Dominant
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about A Rectangle Is A Square Always Sometimes Never . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
