Factors Of X 2 2x 3
Juapaving
Apr 05, 2025 · 5 min read
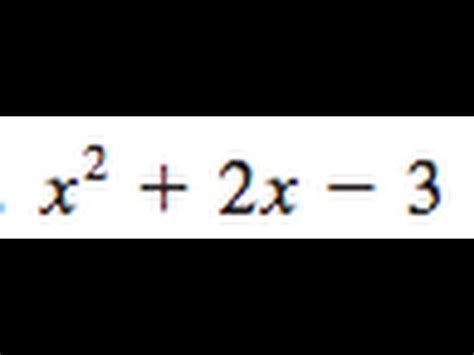
Table of Contents
Factors of x² + 2x - 3: A Comprehensive Guide
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This comprehensive guide delves into the factorization of the quadratic expression x² + 2x - 3, exploring various methods, demonstrating the process step-by-step, and highlighting the importance of factoring in broader mathematical contexts. We'll cover not only the mechanics but also the underlying mathematical concepts.
Understanding Quadratic Expressions
Before we dive into factoring x² + 2x - 3, let's establish a clear understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0. In our case, a = 1, b = 2, and c = -3.
Factoring: The Process of Decomposition
Factoring is the process of breaking down a mathematical expression into simpler components that, when multiplied together, yield the original expression. It's like reverse multiplication. For quadratic expressions, factoring helps simplify equations, solve for unknown variables, and understand the behavior of the corresponding quadratic function.
Method 1: The AC Method (for Factoring Trinomials)
The AC method is a systematic approach to factoring quadratic trinomials (expressions with three terms) of the form ax² + bx + c. Here's how it works for x² + 2x - 3:
-
Identify a, b, and c: In our expression, a = 1, b = 2, and c = -3.
-
Find the product ac: ac = 1 * (-3) = -3.
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 2 (the value of b) and multiply to -3 (the value of ac). These numbers are 3 and -1. (3 + (-1) = 2 and 3 * (-1) = -3).
-
Rewrite the middle term: Rewrite the middle term (2x) using the two numbers we found: x² + 3x - x - 3.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair: x(x + 3) - 1(x + 3)
-
Factor out the common binomial: Notice that (x + 3) is common to both terms. Factor it out: (x + 3)(x - 1).
Therefore, the factored form of x² + 2x - 3 is (x + 3)(x - 1).
Method 2: Trial and Error
This method involves systematically trying different pairs of binomial factors until you find the pair that multiplies to give the original quadratic expression. It's faster for simpler quadratics but can become more time-consuming for more complex ones.
Since the coefficient of x² is 1, we know that the factors will be of the form (x + p)(x + q), where p and q are constants. We need to find p and q such that p + q = 2 (the coefficient of x) and pq = -3 (the constant term). Through trial and error (considering pairs of factors of -3, such as 3 and -1, -3 and 1), we quickly arrive at (x + 3)(x - 1).
Method 3: Using the Quadratic Formula
While primarily used to solve quadratic equations, the quadratic formula can also indirectly help us find the factors. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For x² + 2x - 3, a = 1, b = 2, and c = -3. Substituting these values into the quadratic formula gives:
x = [-2 ± √(2² - 4 * 1 * -3)] / (2 * 1) = [-2 ± √16] / 2 = [-2 ± 4] / 2
This gives us two solutions: x = 1 and x = -3.
Since the solutions are 1 and -3, the factors are (x - 1) and (x + 3). This confirms our previous results. Note that this method is less direct than the AC method or trial and error for finding factors.
Verifying the Factors
To ensure the accuracy of our factoring, we can expand the factors (x + 3)(x - 1) using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * -1 = -x
- Inner: 3 * x = 3x
- Last: 3 * -1 = -3
Combining the terms, we get x² + 3x - x - 3 = x² + 2x - 3, which is our original quadratic expression. This verification confirms that our factoring is correct.
The Significance of Factoring
The ability to factor quadratic expressions is crucial for various mathematical applications, including:
-
Solving Quadratic Equations: Setting the factored quadratic expression equal to zero allows us to easily solve for x, finding the roots or zeros of the quadratic equation. In our case, (x + 3)(x - 1) = 0 implies x = -3 or x = 1.
-
Graphing Quadratic Functions: The roots of the quadratic equation (the values of x where the function equals zero) represent the x-intercepts of the parabola representing the quadratic function y = x² + 2x - 3. Knowing the factors allows us to quickly locate these intercepts.
-
Simplifying Algebraic Expressions: Factoring can simplify more complex algebraic expressions, making them easier to manipulate and solve.
-
Calculus: Factoring plays a vital role in various calculus concepts, including finding derivatives and integrals.
-
Real-world Applications: Quadratic equations and their solutions appear in numerous real-world applications, such as projectile motion, optimization problems, and modeling various physical phenomena. The ability to factor these equations is crucial for solving these real-world problems.
Exploring Further: More Complex Quadratic Expressions
While x² + 2x - 3 is a relatively straightforward quadratic to factor, the techniques discussed here—the AC method, trial and error, and utilizing the quadratic formula—are applicable to more complex quadratic expressions with larger coefficients and potentially leading to irrational or complex roots. The fundamental principles remain the same: finding two numbers that satisfy specific conditions related to the coefficients of the quadratic expression.
Conclusion: Mastering Quadratic Factoring
Mastering the art of factoring quadratic expressions, such as x² + 2x - 3, is essential for success in algebra and beyond. Understanding the various methods—the AC method, trial and error, and the indirect use of the quadratic formula—provides a robust toolkit for tackling a wide range of quadratic expressions. Remembering the significance of factoring in solving equations, graphing functions, and simplifying expressions will solidify your understanding and empower you to confidently approach more challenging mathematical problems. The ability to efficiently factor quadratic expressions is a critical building block for higher-level mathematical concepts.
Latest Posts
Latest Posts
-
Lines Of Symmetry For A Hexagon
Apr 06, 2025
-
What Is 0 5 Of An Hour
Apr 06, 2025
-
Least Common Multiple Of 12 And 5
Apr 06, 2025
-
Cross Section Of A Sphere Parallel Perpendicular And Diagonal
Apr 06, 2025
-
The Main Circuit Board Of A Computer Is Called The
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Factors Of X 2 2x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
