Cross Section Of A Sphere Parallel Perpendicular And Diagonal
Juapaving
Apr 06, 2025 · 7 min read
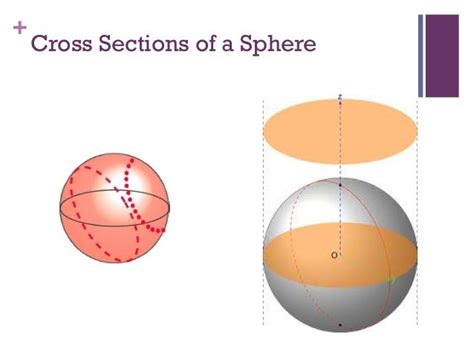
Table of Contents
Cross Section of a Sphere: Parallel, Perpendicular, and Diagonal Planes
Understanding the cross-sections of a sphere is crucial in various fields, from geometry and mathematics to engineering and design. A sphere's cross-section is the shape formed when a plane intersects the sphere. The shape of this cross-section depends entirely on the orientation of the intersecting plane relative to the sphere's center. This article will comprehensively explore the cross-sections of a sphere created by parallel, perpendicular, and diagonal planes, delving into their geometric properties and applications.
Understanding the Sphere and its Geometry
Before diving into the different types of cross-sections, let's establish a firm understanding of the sphere itself. A sphere is a perfectly round geometrical object in three-dimensional space. It is defined as the set of all points in three-dimensional space that are equidistant from a given point, called the center. This equidistant distance is known as the radius (r) of the sphere. A line segment connecting any two points on the sphere's surface and passing through the center is called a diameter (d), and its length is twice the radius (d = 2r).
Cross-Sections: The Intersection of Plane and Sphere
The beauty of a sphere lies in the diverse range of shapes that can be created by intersecting it with a plane. The key factor determining the resulting shape is the relationship between the plane and the sphere's center. We'll examine three fundamental cases:
1. Parallel Cross-Sections
A plane parallel to the sphere's surface will always produce a circular cross-section. This is because any plane parallel to the sphere's surface will be equidistant from the center at all points of intersection. The size of the circle depends on the distance of the parallel plane from the sphere's center.
-
Maximum Cross-Section: If the parallel plane passes through the center of the sphere, the resulting circle is the great circle. This is the largest possible circular cross-section, with a radius equal to the sphere's radius (r) and a diameter equal to the sphere's diameter (2r). The great circle divides the sphere into two equal hemispheres.
-
Smaller Cross-Sections: As the parallel plane moves away from the center, the radius of the resulting circular cross-section decreases. The further the plane is from the center, the smaller the circle becomes, until the plane is tangent to the sphere – at this point, the circle becomes a single point.
Applications of Parallel Cross-Sections:
The concept of parallel cross-sections is vital in various practical applications. Imagine slicing an orange: each slice represents a parallel cross-section. Similarly, in cartography, creating maps of the Earth (which is approximately a sphere) involves projecting sections of the Earth's surface onto a plane, utilizing principles of parallel cross-sections.
2. Perpendicular Cross-Sections
A plane perpendicular to a diameter of the sphere will also create a circular cross-section. This is because, regardless of the plane's position, the distances from the center to all points of intersection on the sphere's surface remain equal.
- Diameter Variation: The diameter of the resulting circle will vary depending on the plane's position. If the perpendicular plane passes through the center of the sphere, it will create a great circle. If it intersects the sphere at any other point along the diameter, it will create a smaller circle.
Applications of Perpendicular Cross-Sections:
The creation of perpendicular cross-sections is evident in various manufacturing processes. For example, cutting a cylindrical pipe (a shape related to the sphere) perpendicular to its length yields a circular cross-section. This understanding is essential in tasks like pipe fitting and structural analysis.
3. Diagonal Cross-Sections
A diagonal plane, in this context, refers to any plane that is neither parallel nor perpendicular to the sphere's diameter. These planes intersect the sphere to create an elliptical cross-section.
-
Ellipse Properties: The ellipse's shape is defined by its major and minor axes. The major axis is the longest diameter of the ellipse, and the minor axis is the shortest diameter. The lengths of these axes depend on the angle of the diagonal plane relative to the sphere's diameter and the distance of the plane from the center. The more slanted the plane, the more elongated the ellipse becomes.
-
Special Case: When the diagonal plane is tangent to the sphere, the ellipse degenerates into a line segment (a highly elongated ellipse where the minor axis is zero).
Applications of Diagonal Cross-Sections:
Understanding diagonal cross-sections is crucial in areas like 3D modeling and computer graphics. Creating realistic 3D representations often involves calculating and rendering elliptical cross-sections to simulate curved surfaces accurately.
Mathematical Representation
The mathematical description of these cross-sections helps solidify our understanding. Consider a sphere centered at the origin (0, 0, 0) with radius r. Its equation is given by:
x² + y² + z² = r²
Parallel Cross-Sections: A plane parallel to the xy-plane, at a distance 'h' from the origin, has the equation z = h. Substituting this into the sphere's equation yields:
x² + y² = r² - h²
This is the equation of a circle with radius √(r² - h²).
Perpendicular Cross-Sections: A plane perpendicular to the z-axis, passing through a point (0,0,h), would intersect the sphere to form a circle with radius √(r² - h²). The equation will be similar to the parallel cross-section case.
Diagonal Cross-Sections: A diagonal plane does not have a simple equation to describe the resultant ellipse directly. The equation would involve a more complex system of equations, potentially involving rotation matrices depending on the orientation of the plane.
Practical Applications Across Various Disciplines
The concepts of sphere cross-sections extend far beyond pure geometry and find practical application in numerous fields:
-
Engineering and Design: Understanding cross-sections is vital for designing pipes, tanks, domes, and other curved structures. Calculating stresses and strains in these structures requires accurate representation of their cross-sections.
-
Medicine: Medical imaging techniques like MRI and CT scans utilize cross-sectional views to visualize internal organs and structures. Interpreting these images depends heavily on understanding the geometries of the resulting cross-sections.
-
Astronomy: Studying the cross-sections of celestial bodies, such as planets and stars, helps scientists understand their internal structures and composition. Analyzing light curves from eclipsing binary stars also involves understanding how the cross-sections change over time.
-
Architecture: In architecture, understanding cross-sections is necessary for designing curved roofs, vaults, and other architectural elements. This allows architects to ensure structural integrity and aesthetic appeal.
-
Manufacturing: Many industrial processes involve cutting or machining spherical or near-spherical objects. The shape of the resulting cross-section influences the properties of the product and the efficiency of the process.
Advanced Concepts and Further Exploration
-
Stereographic Projection: This technique involves projecting points from a sphere onto a plane, providing a useful method for mapping spherical surfaces.
-
Solid Geometry: The study of volumes and surface areas related to spheres and their cross-sections builds upon the foundation laid by understanding their geometric properties.
-
Calculus and Integration: Calculating volumes of irregular shapes created by intersecting a sphere with complex surfaces often utilizes techniques from calculus and integration.
Conclusion
The study of the cross-sections of a sphere, whether parallel, perpendicular, or diagonal, reveals the rich interplay between geometry and real-world applications. From the simple circle to the elegant ellipse, each cross-section provides insights into the sphere's inherent properties and enables the understanding and analysis of complex systems across various disciplines. Mastering these concepts lays a strong foundation for further exploration in geometry, mathematics, and their applications in numerous fields. The diverse range of applications highlights the importance of understanding this fundamental concept, allowing for more accurate modeling, design, and analysis in a vast array of fields. A thorough understanding of sphere cross-sections is essential for professionals in various fields, highlighting its importance as a cornerstone of geometrical knowledge.
Latest Posts
Latest Posts
-
How Many Lines Of Symmetry Does A Octagon Have
Apr 07, 2025
-
How Many Cups Is 6 Quarts Of Water
Apr 07, 2025
-
System Of Linear Equations Practice Problems
Apr 07, 2025
-
Lcm Of 6 7 And 8
Apr 07, 2025
-
What Organisms Need To Be The Fittest To Survive
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Cross Section Of A Sphere Parallel Perpendicular And Diagonal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.