Least Common Multiple Of 7 And 11
Juapaving
Apr 03, 2025 · 5 min read
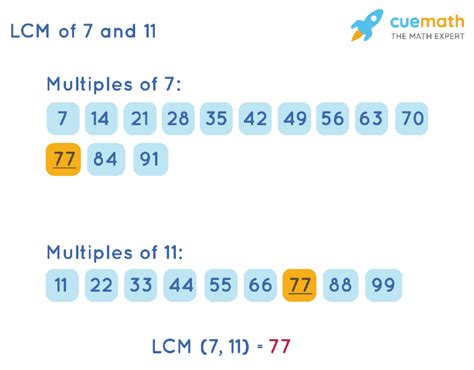
Table of Contents
Unveiling the Least Common Multiple (LCM) of 7 and 11: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and their applications provides a richer understanding of number theory and its relevance in various fields. This article delves into the LCM of 7 and 11, exploring different methods of calculation, its significance in mathematics, and practical applications in real-world scenarios.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with broad applications in various mathematical areas and real-world problems. Understanding the LCM is crucial for simplifying fractions, solving problems related to cycles and periodic events, and even in more advanced areas like abstract algebra.
Key Characteristics of LCM
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by all the numbers involved.
- Minimality: It's the smallest positive integer satisfying the divisibility condition.
- Uniqueness: For a given set of integers, there is only one LCM.
Calculating the LCM of 7 and 11
Since 7 and 11 are both prime numbers, finding their LCM is particularly straightforward. Let's explore several methods:
Method 1: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. This method is particularly useful when dealing with larger numbers or sets of numbers.
- Prime factorization of 7: 7 (7 is a prime number, so its only prime factor is itself)
- Prime factorization of 11: 11 (11 is a prime number)
Since 7 and 11 share no common prime factors, their LCM is simply the product of the two numbers.
LCM(7, 11) = 7 * 11 = 77
Method 2: Listing Multiples
This method involves listing the multiples of each number until a common multiple is found. While effective for smaller numbers, it becomes less efficient with larger numbers.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84...
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88...
The smallest common multiple in both lists is 77.
LCM(7, 11) = 77
Method 3: Formula Using Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are related by the following formula:
LCM(a, b) * GCD(a, b) = a * b
Since 7 and 11 are both prime numbers and share no common factors other than 1, their GCD is 1.
Therefore:
LCM(7, 11) * GCD(7, 11) = 7 * 11 LCM(7, 11) * 1 = 77 LCM(7, 11) = 77
Significance and Applications of LCM
The LCM has far-reaching implications across various mathematical domains and practical applications:
1. Fraction Simplification and Addition/Subtraction
Finding a common denominator when adding or subtracting fractions requires calculating the LCM of the denominators. For instance, adding 1/7 and 1/11 would require finding the LCM of 7 and 11, which is 77.
2. Cyclic Events and Periodic Phenomena
The LCM is essential in solving problems involving cyclical events that occur at different intervals. Consider two machines that operate on cycles of 7 and 11 hours respectively. The LCM (77) represents the time it takes for both machines to simultaneously complete their cycles.
3. Scheduling and Planning
In project management or scheduling, the LCM can help determine the optimal time for events that repeat at different intervals. Imagine two events that happen every 7 days and 11 days respectively. The LCM, 77, indicates when both events will coincide again.
4. Music Theory
In music theory, the LCM is used to calculate the least common multiple of the denominators of different rhythmic values. This helps find the shortest duration that represents a complete cycle of rhythmic patterns.
5. Gear Ratios and Mechanical Systems
In engineering and mechanics, LCM is crucial in designing gear ratios and other systems involving repetitive movements. Understanding how different components with varying periodic motions interact can optimize efficiency and minimize wear and tear.
6. Computer Science and Algorithms
The LCM concept plays a vital role in various algorithms and data structures, particularly in areas concerning synchronization, scheduling tasks and resource management.
Advanced Concepts Related to LCM
For those interested in delving deeper, here are some advanced concepts connected to LCM:
-
Least Common Multiple of more than two numbers: The principle extends to finding the LCM of multiple integers. Prime factorization becomes increasingly useful in such cases.
-
Euclidean Algorithm: This efficient algorithm for finding the greatest common divisor (GCD) can be combined with the formula relating LCM and GCD to calculate the LCM.
-
Modular Arithmetic: The LCM plays a role in modular arithmetic, particularly in solving congruences and analyzing cyclical patterns.
-
Abstract Algebra: The concept of LCM extends to more abstract algebraic structures, providing a foundation for understanding ideal theory and module theory.
Conclusion: The Ubiquitous LCM
The least common multiple of 7 and 11, calculated to be 77, is more than just a simple arithmetic result. It exemplifies a fundamental concept that permeates various areas of mathematics and finds practical applications in diverse fields. Understanding the LCM and its methods of calculation empowers us to solve problems involving cycles, repetitions, and periodic events, further highlighting its significance in both theoretical and practical contexts. Whether simplifying fractions, scheduling tasks, or analyzing cyclical systems, the LCM is a powerful tool that underscores the interconnectedness and elegance of mathematics. Through its diverse applications, it demonstrates the practical and theoretical relevance of seemingly simple mathematical concepts. Exploring the LCM further opens doors to understanding more complex mathematical structures and their far-reaching implications.
Latest Posts
Latest Posts
-
4 Kingdoms In The Domain Eukarya
Apr 03, 2025
-
How Many Inches Is In One Meter
Apr 03, 2025
-
Most Abundant Metal In The Earth Crust
Apr 03, 2025
-
Who Is Credited For Discovering Cells
Apr 03, 2025
-
Is 7 A Prime Or Composite Number
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 7 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
