Electric Field At The End Of A Charged Wire
Juapaving
Apr 05, 2025 · 6 min read
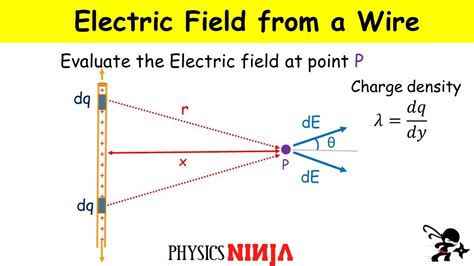
Table of Contents
Electric Field at the End of a Charged Wire: A Deep Dive
The electric field, a fundamental concept in electromagnetism, describes the influence of a charged object on its surroundings. Understanding this field is crucial in numerous applications, from designing electronic circuits to understanding the behavior of charged particles in accelerators. While the electric field surrounding a uniformly charged infinite wire is relatively straightforward to calculate using Gauss's law, the situation becomes significantly more complex when considering a finite wire, especially at its ends. This article delves deep into the intricacies of calculating and understanding the electric field at the end of a charged wire.
The Challenges of a Finite Wire
Unlike an infinitely long wire, where the electric field is purely radial and easily calculated, a finite wire presents several challenges:
-
Non-Uniformity: The electric field isn't uniform along the wire's length, especially near the ends. The charge distribution might not even be perfectly uniform along the wire's length due to end effects.
-
Integration Complexity: Calculating the electric field requires integrating the contributions from infinitesimal charge elements along the wire's length. This integration becomes significantly more complex than in the infinite wire case due to the changing distance and angle between the charge element and the observation point.
-
End Effects: The electric field lines near the ends of the wire are significantly distorted compared to the relatively uniform radial field of an infinite wire. This distortion is a direct consequence of the lack of surrounding charge to cancel out the field components. The field lines are no longer purely radial but exhibit a significant curvature, especially close to the end.
-
Approximations: Obtaining an exact analytical solution for the electric field at the end of a charged wire is generally impossible. Approximation methods, such as numerical integration or considering the wire as a collection of point charges, are often employed.
Approaches to Calculating the Electric Field
Several methods can be employed to approximate the electric field at the end of a charged wire, each with its strengths and limitations:
1. Direct Integration
This method involves integrating the contribution of each infinitesimal charge element along the wire. Consider a thin wire of length 'L' with a uniform linear charge density λ. We want to find the electric field at a point P located at a distance 'r' from one end of the wire, along the perpendicular bisector of the wire. This is a complex problem, mathematically speaking. The integral involves complicated trigonometric functions and often requires numerical techniques for evaluation. The resulting expression will not be a closed-form solution, typically needing numerical methods (like Simpson's rule or Gaussian quadrature) to be evaluated.
2. Numerical Methods
Numerical methods, such as the finite element method (FEM) or the boundary element method (BEM), offer powerful tools for approximating the electric field. These methods discretize the wire into a series of small segments, treating each segment as a point charge or a dipole. The electric field at the desired point is then calculated by summing the contributions from all segments. The accuracy of these methods depends on the fineness of the discretization; finer meshes lead to more accurate results but increase computational cost.
-
Finite Element Method (FEM): Divides the problem domain into small elements and solves the differential equations that govern the electric field within each element. It's particularly suitable for complex geometries and inhomogeneous materials.
-
Boundary Element Method (BEM): Focuses on the boundaries of the problem domain, making it computationally efficient for problems with simple geometries. It converts the governing differential equations into integral equations, reducing the dimension of the problem.
3. Method of Images
The method of images is a powerful technique for solving electrostatics problems involving conductors. While not directly applicable to an isolated charged wire, it becomes relevant if the wire is placed near a conducting plane. The method involves creating "image charges" which simulate the effect of the conductor on the original charge distribution. This technique simplifies the calculation of the electric field significantly. The image charges are usually placed symmetrically with respect to the conducting plane.
4. Approximation using Point Charges
This method approximates the charged wire as a collection of discrete point charges. The wire is divided into several segments, and each segment is treated as a point charge located at its center. The total electric field at a given point is then calculated by summing the individual contributions of these point charges. The accuracy of this approximation increases as the number of point charges increases. However, it's important to note that this method provides only an approximate solution and its accuracy depends heavily on the number of segments used.
Implications and Applications
Understanding the electric field at the end of a charged wire has significant implications across various fields:
-
Electrostatic Discharge (ESD) Protection: In electronics, understanding the high electric field concentration at the ends of conductors is crucial in designing effective ESD protection circuits. This prevents damage to sensitive electronic components caused by sudden electrostatic discharges.
-
High-Voltage Engineering: Designing high-voltage systems requires meticulous calculations of electric field strength to prevent electrical breakdown in air or insulation materials. The high field concentration at conductor ends is a key consideration.
-
Particle Accelerators: The behavior of charged particles in particle accelerators is heavily influenced by the electric fields they experience. Accurate models of electric fields, including those at the ends of electrodes, are essential for precise control of particle trajectories.
-
Antenna Design: The radiation pattern of antennas is directly related to the distribution of electric and magnetic fields. Understanding the electric field at the ends of antenna elements is crucial for optimal antenna design and performance.
Conclusion
Determining the electric field at the end of a charged wire is a challenging problem that doesn't have a simple, closed-form analytical solution. Various approximation techniques, including numerical methods and discrete charge representations, are employed to model this field. The high electric field concentration at these ends has significant implications in numerous applications, ranging from electrostatic discharge protection to high-voltage engineering and particle accelerator design. A deeper understanding of this phenomenon continues to be crucial for advances in many scientific and engineering disciplines. Further research and advancements in computational techniques will likely improve the accuracy and efficiency of predicting and utilizing the complex electric field at the end of a charged wire. The exploration of more sophisticated numerical models, incorporating non-uniform charge distribution and other real-world effects, will offer even more accurate results. The continuous development of this field is driven by the increasing need for precision in various applications of electromagnetism.
Latest Posts
Latest Posts
-
Difference Between Quartz And Quartz Glass
Apr 05, 2025
-
Words That Start With A Z
Apr 05, 2025
-
How Much Is 70 Cm In Inches
Apr 05, 2025
-
Benedicts Reagent Is Used To Identify Which Of The Following
Apr 05, 2025
-
What Is A Positively Charged Ion Called
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Electric Field At The End Of A Charged Wire . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
