Does A Rhombus Have Parallel Lines
Juapaving
Apr 05, 2025 · 5 min read
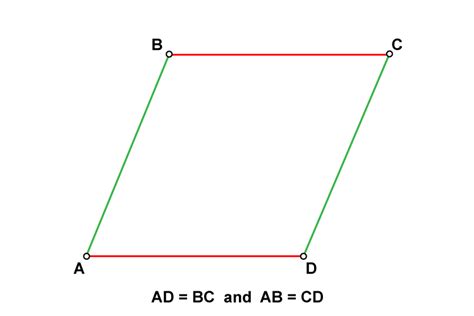
Table of Contents
Does a Rhombus Have Parallel Lines? A Comprehensive Exploration of Quadrilateral Geometry
The question, "Does a rhombus have parallel lines?" might seem simple at first glance. However, a thorough understanding requires delving into the fundamental properties of rhombuses and their relationship to other quadrilaterals. This comprehensive article will explore this question in detail, examining the defining characteristics of rhombuses, comparing them to related shapes, and providing practical examples and applications.
Understanding the Rhombus: A Definition
A rhombus, also known as a diamond, is a special type of quadrilateral. A quadrilateral is any polygon with four sides. What distinguishes a rhombus from other quadrilaterals are its unique properties:
-
All sides are equal in length: This is the defining characteristic. If you measure each side of a rhombus, they will all be the same length.
-
Opposite sides are parallel: This is crucial to answering our initial question. The opposite sides of a rhombus are parallel to each other. This parallelism is a direct consequence of the equal side lengths.
-
Opposite angles are equal: The angles opposite each other in a rhombus are congruent (equal in measure).
-
Adjacent angles are supplementary: Adjacent angles (angles next to each other) add up to 180 degrees. This is a property of all parallelograms, and since a rhombus is a parallelogram (as we'll discuss later), this holds true.
The Relationship Between Rhombuses and Parallelograms
A rhombus is a specific type of parallelogram. A parallelogram is a quadrilateral where both pairs of opposite sides are parallel. Therefore, all rhombuses are parallelograms, but not all parallelograms are rhombuses. Think of it like this: all squares are rectangles, but not all rectangles are squares.
This relationship is key to understanding the parallel lines in a rhombus. Because a rhombus is a parallelogram, it inherently possesses the property of having opposite sides that are parallel. This fact directly answers our main question: Yes, a rhombus has parallel lines.
Visualizing Parallel Lines in a Rhombus
Imagine a rhombus drawn on a piece of paper. You can visually identify the parallel lines. If you were to extend the opposite sides, they would never intersect. This is a characteristic of parallel lines. You can use a ruler to reinforce this visualization. Place the ruler along one side and you'll see that the opposite side aligns perfectly, confirming their parallelism.
Furthermore, consider the lines of symmetry within a rhombus. A rhombus has two lines of symmetry that pass through opposite vertices (corners) and bisect (divide equally) the opposite angles. These lines of symmetry themselves are not necessarily parallel to the sides, but they help to further illustrate the structural symmetry and the resulting parallelism of opposite sides.
Comparing Rhombuses to Other Quadrilaterals
To fully appreciate the significance of parallel lines in a rhombus, let's compare it to other quadrilaterals:
-
Square: A square is a special case of a rhombus (and a rectangle). It possesses all the properties of a rhombus, including parallel opposite sides, but adds the extra condition that all angles are right angles (90 degrees).
-
Rectangle: A rectangle has opposite sides that are parallel and equal in length, but its adjacent sides are not necessarily equal. Therefore, a rectangle is a parallelogram but not necessarily a rhombus.
-
Trapezoid: A trapezoid has only one pair of parallel sides. This contrasts sharply with a rhombus, which has two pairs of parallel sides.
-
Kite: A kite has two pairs of adjacent sides that are equal in length, but its opposite sides are not parallel. This distinguishes it significantly from a rhombus.
Mathematical Proof of Parallelism in a Rhombus
We can mathematically prove that opposite sides of a rhombus are parallel. This proof leverages the properties of congruent triangles and the definition of parallel lines.
Proof:
Let's consider a rhombus ABCD, where AB = BC = CD = DA. Let's draw the diagonal AC. Now, consider triangles ABC and ADC.
- AB = AD (given - all sides are equal)
- BC = DC (given - all sides are equal)
- AC is common to both triangles
Therefore, triangles ABC and ADC are congruent by the SSS (Side-Side-Side) postulate. Because the triangles are congruent, their corresponding angles are equal. Specifically:
- ∠BAC = ∠DAC
- ∠BCA = ∠DCA
Now, consider lines AB and DC. Since ∠BAC = ∠DAC, these angles are alternate interior angles. If alternate interior angles are equal, then the lines that form them are parallel. Therefore, AB is parallel to DC.
Similarly, consider lines BC and AD. Since ∠BCA = ∠DCA, these are also alternate interior angles. Therefore, BC is parallel to AD.
This proves that opposite sides of a rhombus are indeed parallel.
Real-World Applications of Rhombuses and Parallel Lines
The properties of rhombuses, particularly the parallelism of their opposite sides, find applications in various fields:
-
Engineering: The structural strength of rhombus shapes is utilized in many engineering designs, such as bridges and trusses. The parallel sides contribute to the stability of these structures.
-
Architecture: Rhombuses appear in various architectural designs, often for aesthetic reasons or to create visually interesting patterns. The parallel lines contribute to the structural integrity and the overall design.
-
Art and Design: Rhombuses are common elements in art and design, adding a sense of dynamism and visual interest to various pieces. The parallel lines create a sense of order and structure within the artistic composition.
-
Nature: While not perfectly precise rhombuses, certain natural formations and patterns exhibit rhombus-like characteristics. The parallel line property can be observed in the arrangements of some crystals and other natural structures.
-
Textiles: Rhombus patterns are widely used in textile designs, adding texture and visual appeal to clothing and other fabrics.
Conclusion: The Definitive Answer
The answer to the question, "Does a rhombus have parallel lines?" is a resounding yes. This fundamental property is a direct consequence of the rhombus's defining characteristic: all sides are equal in length. This parallelism is inherited from the rhombus's classification as a parallelogram, and it plays a crucial role in its geometric properties and real-world applications. Understanding this property is fundamental to grasping the geometry of rhombuses and their relationships to other quadrilaterals. The mathematical proof solidifies this understanding, highlighting the logical connection between the equal side lengths and the parallel opposite sides. The numerous applications of rhombuses in various fields further illustrate the practical importance of this fundamental geometric property.
Latest Posts
Latest Posts
-
Bronsted Lowry Vs Lewis Vs Arrhenius
Apr 05, 2025
-
Name Two Constituents Of Baking Powder
Apr 05, 2025
-
The Study Of Tissue Is Known As
Apr 05, 2025
-
5 Is What Percent Of 8
Apr 05, 2025
-
What Is 104 Fahrenheit In Celsius
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Does A Rhombus Have Parallel Lines . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
