Does A Rhombus Have 4 Right Angles
Juapaving
Apr 05, 2025 · 5 min read
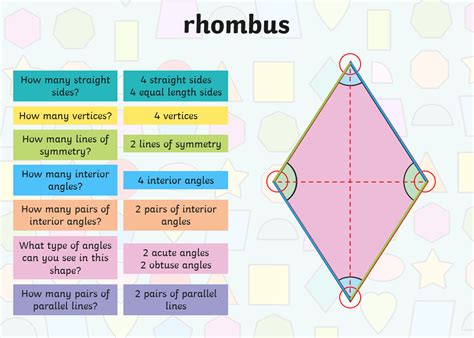
Table of Contents
Does a Rhombus Have 4 Right Angles? Understanding Quadrilateral Properties
The question of whether a rhombus possesses four right angles is a fundamental concept in geometry, often causing confusion among students. The short answer is: not necessarily. While a rhombus shares some characteristics with a rectangle (and even a square), the defining feature that distinguishes it is its equal side lengths, not its angles. Let's delve deeper into the properties of rhombuses and other quadrilaterals to clarify this crucial distinction.
Understanding Quadrilaterals: A Family of Shapes
Before we focus specifically on rhombuses, it's essential to understand the broader family of quadrilaterals. Quadrilaterals are polygons with four sides and four angles. Within this family, several specific types exist, each with its unique properties:
1. Trapezoids: The General Case
Trapezoids are the most general type of quadrilateral. They are defined simply as having at least one pair of parallel sides. These parallel sides are called bases, while the other two sides are called legs. There's no restriction on the lengths of the sides or the measures of the angles.
2. Parallelograms: Parallel Sides Take Center Stage
Parallelograms are quadrilaterals with two pairs of parallel sides. This property leads to several important consequences:
- Opposite sides are equal in length: This is a direct result of the parallel sides.
- Opposite angles are equal in measure: This stems from the parallel lines and transversal formed by the sides.
- Consecutive angles are supplementary: This means that any two angles sharing a side add up to 180 degrees.
3. Rectangles: Right Angles Enter the Picture
Rectangles are parallelograms with the added condition that all four angles are right angles (90 degrees). This additional constraint ensures that the opposite sides are parallel and equal in length, inheriting the properties of parallelograms.
4. Rhombuses: All Sides Equal
Rhombuses are parallelograms where all four sides are of equal length. This characteristic is their defining feature. Note that this doesn't automatically imply right angles.
5. Squares: The Perfect Combination
Squares are the most specialized type of quadrilateral. They are both rectangles and rhombuses. This means they possess all the properties of both: four right angles and four equal sides.
The Rhombus: A Deeper Dive into its Properties
Now, let's focus specifically on the rhombus. Remember, the crucial defining property of a rhombus is that all four sides are congruent (equal in length). This leads to several unique characteristics:
- Diagonals bisect each other: The two diagonals of a rhombus intersect at a point that divides each diagonal into two equal segments.
- Diagonals are perpendicular bisectors: This means that the diagonals intersect at a right angle, and each diagonal bisects (cuts in half) the other.
- Opposite angles are equal: As a rhombus is a parallelogram, this property is inherited.
- Consecutive angles are supplementary: Again, this is inherited from its parallelogram nature.
Crucially, a rhombus does not have to have four right angles. While a square is a special case of a rhombus (a rhombus with right angles), most rhombuses will have angles other than 90 degrees. Think of a tilted square – it still maintains equal side lengths, but the angles are no longer right angles; it is still a rhombus.
Visualizing Rhombuses: Examples and Non-Examples
To solidify the understanding, let's consider some visual examples:
Example 1: A Square (Special Case of Rhombus)
Imagine a square. All four sides are equal, and all four angles are 90 degrees. This is a special case of a rhombus where all angles are right angles.
Example 2: A Tilted Square (Typical Rhombus)
Now, imagine taking that same square and tilting it. The side lengths remain equal, but the angles are no longer 90 degrees. This tilted square is a perfect example of a rhombus that does not have four right angles. It retains its equal sides, the defining characteristic of a rhombus.
Example 3: A Rhombus with Obtuse and Acute Angles
Consider a rhombus where two opposite angles are obtuse (greater than 90 degrees) and the other two opposite angles are acute (less than 90 degrees). This is another clear example showcasing that a rhombus need not possess right angles. The equality of sides is the primary characteristic.
The Importance of Precise Definitions in Geometry
The distinction between a rhombus and a square (or rectangle) highlights the importance of precise definitions in geometry. Each quadrilateral type builds upon the properties of simpler shapes, but each has its own unique characteristics. Failing to appreciate these distinctions can lead to misconceptions and errors in geometrical problem-solving.
Connecting Rhombuses to Real-World Examples
Rhombuses aren't just abstract shapes found in geometry textbooks. They have numerous real-world applications:
- Crystals: Many naturally occurring crystals exhibit rhombic structures.
- Tiles and Mosaics: Rhombus-shaped tiles are often used in artistic designs.
- Engineering and Design: The properties of rhombuses can be leveraged in various engineering and architectural designs.
- Art and Architecture: The visually appealing properties of rhombuses lead to their frequent appearance in art and architecture, creating unique and interesting designs.
Understanding the properties of a rhombus, especially its relationship to squares and other quadrilaterals, provides a solid foundation for further exploration in geometry and its applications.
Conclusion: A Rhombus is Not Always a Square
To reiterate, a rhombus does not have to have four right angles. The defining characteristic of a rhombus is its four equal sides. While a square is a special type of rhombus (one with four right angles), many rhombuses exist with angles other than 90 degrees. This understanding is crucial for accurate geometric reasoning and problem-solving. The careful consideration of definitions and properties is essential to navigate the world of quadrilaterals effectively. Remember the key difference: equal sides for a rhombus, equal sides and right angles for a square. This distinction eliminates any confusion around the question: Does a rhombus have 4 right angles? The answer is definitively: No, not always.
Latest Posts
Latest Posts
-
Buffer Region On A Titration Curve
Apr 06, 2025
-
What Is The Relationship Between Kinetic And Potential Energy
Apr 06, 2025
-
Conversion Of Mechanical Energy To Electrical Energy
Apr 06, 2025
-
Is A Rectangle A Regular Polygon
Apr 06, 2025
-
5 Letter Words Starting With R I
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Does A Rhombus Have 4 Right Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
