Do The Diagonals Of A Kite Bisect Bisect The Angles
Juapaving
Apr 03, 2025 · 5 min read
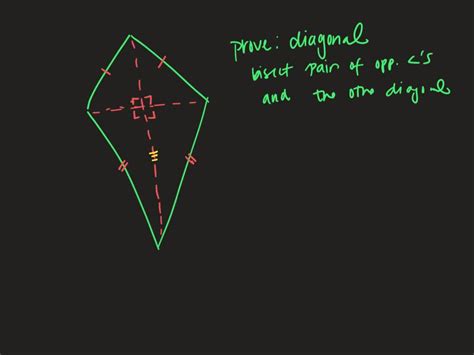
Table of Contents
- Do The Diagonals Of A Kite Bisect Bisect The Angles
- Table of Contents
- Do the Diagonals of a Kite Bisect the Angles? A Comprehensive Exploration
- Defining a Kite: Understanding the Foundation
- Investigating the Diagonals: Bisecting Angles or Not?
- Proof and Geometric Reasoning
- Exploring Related Geometric Concepts
- Real-World Applications of Kite Geometry
- Common Misconceptions and Clarifications
- Conclusion: A Deeper Understanding of Kite Geometry
- Latest Posts
- Latest Posts
- Related Post
Do the Diagonals of a Kite Bisect the Angles? A Comprehensive Exploration
The question of whether the diagonals of a kite bisect its angles is a common one in geometry, often sparking confusion and debate. Understanding this property requires a deep dive into the definition of a kite, its properties, and the implications of its unique structure. This article will provide a comprehensive analysis, exploring not only the answer to the central question but also delving into related geometric concepts and theorems.
Defining a Kite: Understanding the Foundation
Before we delve into the properties of diagonals, let's establish a firm understanding of what constitutes a kite. A kite is a quadrilateral with two pairs of adjacent sides that are congruent. This means that two sides sharing a common vertex are equal in length, while the other two sides, also sharing a vertex, are also equal in length, but not necessarily equal to the first pair.
It's crucial to distinguish a kite from other quadrilaterals. While a rhombus shares the property of having two pairs of equal sides, all its sides are congruent, a characteristic that doesn't apply to kites. Similarly, a square possesses all the characteristics of a kite (and a rhombus) but adds the requirement of having four right angles.
Key Characteristics of a Kite:
- Two pairs of adjacent congruent sides: This is the defining characteristic.
- One pair of opposite angles are congruent: This arises directly from the congruent sides.
- Diagonals intersect at right angles: This is a critical property relevant to our investigation.
- One diagonal bisects the other: Only one diagonal, the one connecting the vertices of the unequal sides, will bisect the other.
Investigating the Diagonals: Bisecting Angles or Not?
Now we arrive at the core question: Do the diagonals of a kite bisect its angles? The answer is nuanced. Only one diagonal of a kite bisects its angles, and that's the diagonal that connects the vertices of the unequal sides. This diagonal acts as a line of symmetry for the kite, dividing it into two congruent triangles. Therefore, the angles formed on either side of this diagonal are indeed equal.
However, the other diagonal, connecting the vertices of the congruent sides, does not bisect the angles. This diagonal divides the kite into two triangles that are not congruent. Consequently, the angles formed on either side of this diagonal are not equal.
Visual Representation: Imagine a kite. Draw both its diagonals. Observe how the diagonal connecting the vertices of the unequal sides divides the kite into two mirror-image triangles. The angles at the vertices where this diagonal intersects are clearly bisected. Now look at the other diagonal. The triangles it creates are clearly not congruent, indicating that the angles are not bisected.
Proof and Geometric Reasoning
Let's delve into a more formal geometric proof to solidify our understanding.
Theorem: In a kite, only the diagonal connecting the vertices of the unequal sides bisects the angles at those vertices.
Proof:
- Consider a kite ABCD, where AB = AD and BC = CD. Let the diagonals intersect at point O.
- Consider triangle ABC and triangle ADC. Since AB = AD and BC = CD (given), and AC is a common side, the triangles are congruent by SSS (Side-Side-Side) congruence.
- Because triangles ABC and ADC are congruent, their corresponding angles are also congruent. Therefore, ∠BAC = ∠DAC and ∠BCA = ∠DCA. This demonstrates that diagonal AC bisects angles A and C.
- Now consider triangle ABO and triangle ADO. While AB = AD (given), we cannot directly assert the congruence of these two triangles. The angles ∠ABO and ∠ADO are generally not equal. This shows that diagonal BD does not bisect angles B and D.
Exploring Related Geometric Concepts
The study of kites touches upon several other important geometric concepts:
- Congruence: Understanding congruence of triangles is fundamental to proving the angle bisecting property of one diagonal.
- Symmetry: The kite possesses a line of symmetry along the diagonal connecting the vertices of the unequal sides.
- Area: The area of a kite can be calculated using the lengths of its diagonals. The formula is: Area = (1/2) * d1 * d2, where d1 and d2 are the lengths of the diagonals.
Real-World Applications of Kite Geometry
The geometry of kites isn't just an abstract mathematical concept; it has practical applications in various fields:
- Engineering: The structural properties of a kite are exploited in bridge designs and other engineering structures.
- Architecture: Kite shapes can be found in architectural designs, both for aesthetic purposes and for structural stability.
- Art and Design: The unique shape and properties of kites make them a source of inspiration for artists and designers.
- Nature: Certain natural formations and structures exhibit kite-like shapes.
Common Misconceptions and Clarifications
It’s important to address some common misconceptions:
- All quadrilaterals with congruent adjacent sides are kites: This is incorrect. The sides must be adjacent not opposite.
- Both diagonals of a kite always bisect each other: This is false. Only one diagonal bisects the other.
- Kites are always symmetrical: Kites have only one line of symmetry (along the diagonal connecting vertices of unequal sides).
Conclusion: A Deeper Understanding of Kite Geometry
This comprehensive exploration has clarified the nuanced answer to the question: Do the diagonals of a kite bisect the angles? The answer is definitively no, but with a crucial qualification: only the diagonal connecting the vertices of the unequal sides bisects the angles at those vertices. This understanding requires a thorough grasp of the kite's defining characteristics and the application of geometric principles such as congruence and symmetry. The properties of kites extend beyond this specific characteristic, encompassing their area calculation, structural implications, and diverse applications across various fields. Through this detailed analysis, we've not only answered the initial question but also significantly enhanced our understanding of the rich geometry of kites.
Latest Posts
Latest Posts
-
What Is The Atomic Mass Of Magnesium
Apr 05, 2025
-
A Pectoral Girdle Consists Of Two Bones The And The
Apr 05, 2025
-
How Many Feet Is 26 Inches
Apr 05, 2025
-
Actin And Myosin Are What Type Of Biological Molecule
Apr 05, 2025
-
Fluid Part Of Blood After Removal Of Corpuscles Is
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Do The Diagonals Of A Kite Bisect Bisect The Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
