Dilated By A Scale Factor Of 1/2
Juapaving
Apr 01, 2025 · 6 min read
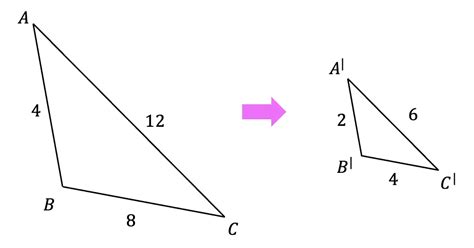
Table of Contents
Dilated by a Scale Factor of 1/2: A Comprehensive Guide to Transformations
Understanding geometric transformations is crucial in various fields, from computer graphics and architecture to physics and mathematics. One fundamental transformation is dilation, which involves resizing a shape while preserving its overall form. This article delves deep into dilation, specifically focusing on dilation by a scale factor of 1/2. We'll explore the process, its mathematical representation, applications, and practical examples.
What is Dilation?
Dilation, in geometry, is a transformation that changes the size of a figure but not its shape. It's a type of similarity transformation, meaning the original figure and the dilated figure are similar—they have the same shape but different sizes. The dilation is performed relative to a fixed point called the center of dilation.
The size change is determined by the scale factor, often denoted by 'k'. If k > 1, the figure is enlarged (an enlargement or expansion). If 0 < k < 1, the figure is reduced (a reduction or contraction). If k = 1, the figure remains unchanged. If k is negative, the figure is enlarged or reduced and reflected across the center of dilation. This article focuses on the case where k = 1/2, representing a reduction.
Key Components of Dilation:
- Center of Dilation: The fixed point around which the dilation occurs. All points are scaled relative to this center.
- Scale Factor (k): The ratio of the distance from the center of dilation to a point in the dilated image to the distance from the center of dilation to the corresponding point in the original image. In our case, k = 1/2.
- Pre-image: The original figure before dilation.
- Image: The figure after dilation.
Dilating by a Scale Factor of 1/2: The Process
When a figure is dilated by a scale factor of 1/2, each point in the figure is moved halfway closer to the center of dilation. This results in a figure that is half the size of the original.
Let's break down the process step-by-step:
-
Identify the Center of Dilation: This is the fixed point around which the transformation takes place. It's usually specified in the problem.
-
Connect Points to the Center: Draw lines connecting each vertex (or key point) of the pre-image to the center of dilation.
-
Find the Midpoint: For each line segment created in step 2, locate the midpoint. This midpoint represents the corresponding point in the dilated image. Since the scale factor is 1/2, the midpoint is exactly halfway between the original point and the center of dilation.
-
Connect the Midpoints: Connect the midpoints found in step 3 to create the dilated image. The resulting image will be similar to the original but half its size.
Mathematical Representation
While the geometric approach is intuitive, a mathematical representation offers precision and allows for calculations involving coordinates.
Let's assume the center of dilation is at the origin (0, 0). If a point (x, y) in the pre-image is dilated by a scale factor of 1/2, its corresponding point (x', y') in the image will be:
(x', y') = (1/2 * x, 1/2 * y)
This formula effectively halves the x and y coordinates of each point in the pre-image, resulting in a smaller image.
If the center of dilation is not at the origin, the calculation becomes slightly more complex. Let's say the center of dilation is at (a, b). Then the formula for the dilated point (x', y') becomes:
(x', y') = (a + 1/2(x - a), b + 1/2(y - b))
This formula first translates the point relative to the center of dilation, then scales it by 1/2, and finally translates it back.
Applications of Dilation with a Scale Factor of 1/2
The application of dilation with a scale factor of 1/2 is widespread across various fields:
1. Computer Graphics and Image Processing:
Reducing the size of images is a common task in image processing. A scale factor of 1/2 effectively reduces the resolution of an image by half, making it smaller and potentially faster to process or transmit.
2. Architecture and Engineering:
Scale models are frequently used in architecture and engineering. A scale factor of 1/2 allows for the creation of a model that is half the size of the actual structure, providing a manageable and convenient representation.
3. Mapmaking and Cartography:
Maps often use different scales to represent geographic areas. A scale factor of 1/2 could be employed to create a smaller-scale map from a larger-scale map, making it more convenient for certain applications.
4. Photography:
Adjusting image size in photo editing software often involves dilating the image by a specific scale factor. Reducing an image by a scale factor of 1/2 is a common method for decreasing file size while retaining image quality.
5. Mathematics and Geometry:
Understanding dilation is crucial for grasping concepts like similarity, congruence, and transformations in geometry. Working with scale factors like 1/2 helps build a strong foundation in these areas.
Examples of Dilation with a Scale Factor of 1/2
Let's illustrate with concrete examples:
Example 1: A Square with vertices at (0,0), (2,0), (2,2), (0,2), and center of dilation at (0,0).
Applying the formula (x', y') = (1/2 * x, 1/2 * y), we get the new vertices: (0,0), (1,0), (1,1), (0,1). This new square is half the size of the original.
Example 2: A Triangle with vertices at (1,1), (3,1), (2,3), and center of dilation at (0,0).
Using the same formula, the new vertices become (0.5, 0.5), (1.5, 0.5), (1, 1.5). Again, the resulting triangle is half the size of the original.
Example 3: A Circle with a radius of 4 and center at (2,2), center of dilation at (0,0).
While the formula directly applies to points, for a circle, we consider the radius. The new radius will be half of the original, meaning the new radius is 2. The center is also dilated, becoming (1,1).
Example 4: Considering a center of dilation that is not the origin.
Let’s take a triangle with vertices A(2,2), B(4,2), C(3,4). The center of dilation is at (1,1). Using the formula (x', y') = (a + 1/2(x - a), b + 1/2(y - b)), where (a,b) = (1,1):
- A'(x', y'): (1 + 1/2(2-1), 1 + 1/2(2-1)) = (1.5, 1.5)
- B'(x', y'): (1 + 1/2(4-1), 1 + 1/2(2-1)) = (2.5, 1.5)
- C'(x', y'): (1 + 1/2(3-1), 1 + 1/2(4-1)) = (2, 2.5)
The new triangle A'B'C' is smaller and similar to the original triangle ABC.
Conclusion
Dilation by a scale factor of 1/2 is a fundamental geometric transformation with significant practical applications. Understanding the process, the mathematical representation, and the diverse applications allows for a deeper appreciation of this key concept in geometry and its relevance in various fields. From creating smaller-scale models to reducing image sizes, this transformation plays a crucial role in many aspects of our technological and physical world. Remember that mastering this concept will enhance your understanding of geometric transformations and their importance in various disciplines. Practice with different shapes and centers of dilation to solidify your understanding.
Latest Posts
Latest Posts
-
Is Boiling A Physical Or Chemical Change
Apr 02, 2025
-
Rectangle Has How Many Lines Of Symmetry
Apr 02, 2025
-
How To Find Recoil In Physics
Apr 02, 2025
-
87 Inches Is How Many Feet
Apr 02, 2025
-
Electrons Are Lost Or Gained During
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Dilated By A Scale Factor Of 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
