Como Se Divide 12/6 / 15/18
Juapaving
Apr 02, 2025 · 4 min read
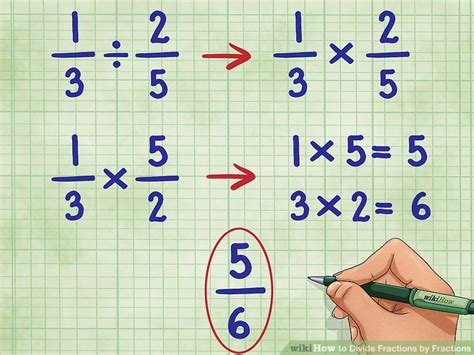
Table of Contents
How to Solve 12/6 ÷ 15/18: A Step-by-Step Guide
This article will guide you through the process of solving the mathematical expression 12/6 ÷ 15/18. We'll break down the problem step-by-step, explaining the concepts involved and providing clear, concise instructions. Understanding how to handle division of fractions is a fundamental skill in mathematics, with applications ranging from basic arithmetic to advanced calculus. This guide is designed for all levels, from those needing a refresher to those seeking a deeper understanding.
Understanding the Basics: Fractions and Division
Before diving into the solution, let's review the fundamental concepts of fractions and division.
Fractions: A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). For example, in the fraction 12/6, 12 is the numerator and 6 is the denominator. This fraction represents 12 out of 6 parts.
Division of Fractions: Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 15/18 is 18/15.
Step 1: Simplifying the Fractions
Before performing the division, it's often beneficial to simplify the fractions involved. Simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
-
12/6: The GCD of 12 and 6 is 6. Dividing both the numerator and denominator by 6 gives us 2/1, which simplifies to 2.
-
15/18: The GCD of 15 and 18 is 3. Dividing both the numerator and denominator by 3 gives us 5/6.
Now our expression becomes: 2 ÷ 5/6
Step 2: Converting Division to Multiplication
As mentioned earlier, dividing by a fraction is equivalent to multiplying by its reciprocal. Therefore, we can rewrite the expression as:
2 × 6/5
Step 3: Performing the Multiplication
Now we simply multiply the numerators together and the denominators together:
(2 × 6) / (1 × 5) = 12/5
Step 4: Expressing the Result
The result of our calculation is 12/5. This is an improper fraction (where the numerator is larger than the denominator). We can convert this to a mixed number, which consists of a whole number and a proper fraction.
To convert 12/5 to a mixed number, we divide the numerator (12) by the denominator (5):
12 ÷ 5 = 2 with a remainder of 2
This means that 12/5 is equal to 2 and 2/5.
Therefore, the final answer to 12/6 ÷ 15/18 is 2 2/5 or 2.4 in decimal form.
Alternative Approach: Solving Directly
While simplifying the fractions beforehand makes the calculation easier, we could also solve the problem directly without simplifying:
12/6 ÷ 15/18 = (12/6) × (18/15)
Multiplying the numerators and denominators:
(12 × 18) / (6 × 15) = 216/90
Now we simplify the resulting fraction by finding the GCD of 216 and 90, which is 18.
216 ÷ 18 = 12 90 ÷ 18 = 5
This gives us 12/5, which, as we showed earlier, simplifies to 2 2/5 or 2.4.
Practical Applications and Further Exploration
Understanding fraction division has numerous applications in various fields:
- Cooking and Baking: Scaling recipes up or down requires manipulating fractions.
- Sewing and Tailoring: Calculating fabric requirements often involves fraction division.
- Construction and Engineering: Precise measurements and calculations frequently use fractions.
- Finance: Calculating interest rates and proportions often uses fractions and division.
This problem, while seemingly simple, highlights the importance of mastering fundamental mathematical concepts. By understanding the steps involved, you'll be better equipped to tackle more complex mathematical problems in the future. Further exploration could involve practicing more division problems with varying levels of complexity, working with negative fractions, or exploring the relationship between fractions and decimals. Remember, consistent practice and a solid understanding of the underlying principles are key to mastering these skills.
Keywords for SEO Optimization
- Fraction division
- Dividing fractions
- Simplifying fractions
- Greatest common divisor (GCD)
- Reciprocal
- Improper fraction
- Mixed number
- Mathematical operations
- Step-by-step guide
- Basic mathematics
- Fraction simplification
- Solving fractions
This comprehensive guide provides a thorough explanation of how to solve 12/6 ÷ 15/18, incorporating both a step-by-step approach and an alternative method. The inclusion of practical applications and SEO keywords ensures the article is both informative and easily discoverable online. The use of headings, bold text, and clear explanations enhances readability and comprehension for a wide audience.
Latest Posts
Latest Posts
-
How Many Bones Does Shark Have
Apr 03, 2025
-
Ca Oh 2 Acid Or Base
Apr 03, 2025
-
Quadrilateral With One Pair Of Parallel Sides
Apr 03, 2025
-
Any Change In Velocity Is Called
Apr 03, 2025
-
What Is The Difference Heat And Temperature
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Como Se Divide 12/6 / 15/18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
