Classify Each Number As Rational Or Irrational
Juapaving
Apr 03, 2025 · 5 min read
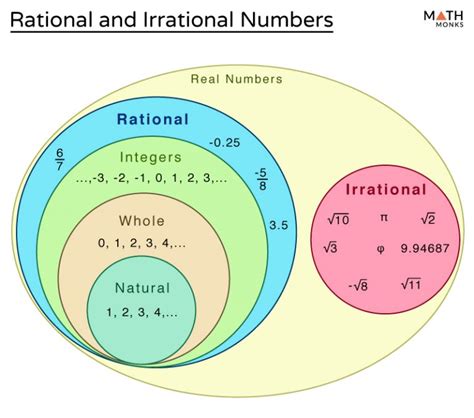
Table of Contents
Classify Each Number as Rational or Irrational: A Comprehensive Guide
Understanding the difference between rational and irrational numbers is fundamental to grasping core concepts in mathematics. This comprehensive guide will delve into the definitions, properties, and examples of both, equipping you with the tools to confidently classify any number. We'll explore various number types, providing clear explanations and numerous examples to solidify your understanding.
What are Rational Numbers?
A rational number is any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not equal to zero. This seemingly simple definition encompasses a vast range of numbers. Let's break it down:
- Integers: These are whole numbers, including positive numbers (1, 2, 3...), negative numbers (-1, -2, -3...), and zero (0).
- Fraction: A fraction represents a part of a whole. The numerator (p) is the top number, representing the part, and the denominator (q) is the bottom number, representing the whole.
Examples of Rational Numbers:
-
Integers: All integers are rational numbers because they can be expressed as a fraction with a denominator of 1. For example, 5 can be written as 5/1, -3 as -3/1, and 0 as 0/1.
-
Fractions: Numbers like 1/2, 3/4, -2/5, and 7/10 are all rational numbers because they are expressed in the p/q format.
-
Terminating Decimals: Decimals that end after a finite number of digits are rational. For example, 0.75 (which is 3/4), 0.2 (which is 1/5), and 2.5 (which is 5/2).
-
Repeating Decimals: Decimals with a repeating pattern of digits are also rational. For instance, 0.333... (which is 1/3), 0.666... (which is 2/3), and 0.142857142857... (which is 1/7). These repeating decimals can be converted into fractions.
Key Characteristics of Rational Numbers:
- They can always be expressed as a fraction.
- Their decimal representation either terminates or repeats.
- They are densely packed on the number line; meaning between any two rational numbers, there's always another rational number.
What are Irrational Numbers?
An irrational number is any real number that cannot be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. This means their decimal representation neither terminates nor repeats; it continues infinitely without any pattern.
Examples of Irrational Numbers:
-
√2 (Square root of 2): This is a classic example. Its decimal representation is approximately 1.41421356..., continuing infinitely without repeating. It cannot be expressed as a fraction of two integers.
-
√3 (Square root of 3): Similar to √2, its decimal representation is non-terminating and non-repeating.
-
√5 (Square root of 5): Another example of a square root of a non-perfect square number.
-
π (Pi): The ratio of a circle's circumference to its diameter. It's approximately 3.14159265..., but the digits continue infinitely without a repeating pattern.
-
e (Euler's number): The base of the natural logarithm. Approximately 2.71828..., it also has a non-terminating, non-repeating decimal representation.
-
Golden Ratio (φ): Approximately 1.6180339887..., it's an irrational number with significant properties in geometry and art.
Key Characteristics of Irrational Numbers:
- They cannot be expressed as a fraction of two integers.
- Their decimal representation is non-terminating and non-repeating.
- They fill in the gaps between rational numbers on the number line.
Distinguishing Between Rational and Irrational Numbers: A Practical Approach
Classifying a number as rational or irrational often involves careful examination of its decimal representation or attempting to express it as a fraction.
1. Decimal Representation:
- Terminating decimals: These are always rational.
- Repeating decimals: These are always rational.
- Non-terminating, non-repeating decimals: These are always irrational.
2. Fraction Representation:
If you can express a number as a fraction p/q, where p and q are integers and q ≠ 0, the number is rational. If you cannot express it in this form, it's irrational. Sometimes, proving a number is irrational requires advanced mathematical techniques.
3. Square Roots:
The square root of a perfect square (e.g., √4 = 2, √9 = 3, √16 = 4) is rational. The square root of a non-perfect square (e.g., √2, √3, √5) is irrational. This principle extends to other roots as well.
Examples: Classifying Numbers
Let's classify some numbers to solidify our understanding:
1. 0.75: This is a terminating decimal, so it's rational. It can be written as 3/4.
2. -3: This is an integer, and all integers are rational. It can be written as -3/1.
3. 2/9: This is a fraction, making it rational. Its decimal representation is 0.222... (a repeating decimal).
4. √16: This is the square root of a perfect square (4 x 4 = 16), so it's rational (it equals 4).
5. √7: This is the square root of a non-perfect square, making it irrational.
6. π (Pi): This is a well-known irrational number.
7. 0.121212...: This is a repeating decimal, so it's rational.
8. 0.1010010001...: This decimal is non-terminating and non-repeating, making it irrational.
9. e (Euler's Number): This is an irrational number.
10. 3.14: While this is an approximation of π, it is a terminating decimal, and hence rational. It’s important to note the difference between the approximation and the actual value of Pi.
Advanced Concepts and Further Exploration
The distinction between rational and irrational numbers is crucial for more advanced mathematical concepts. Understanding this foundational difference will help you in areas such as:
- Real Number System: Rational and irrational numbers together constitute the set of real numbers.
- Calculus: The concept of limits and continuity often involves dealing with both rational and irrational numbers.
- Number Theory: Many theorems and proofs in number theory rely on the properties of rational and irrational numbers.
- Algebra: Solving equations and inequalities may involve working with both rational and irrational solutions.
Conclusion: Mastering Rational and Irrational Numbers
Successfully classifying numbers as rational or irrational depends on a strong understanding of their definitions and properties. By carefully examining decimal representations and attempting to express numbers as fractions, you can confidently distinguish between these two fundamental categories of numbers. Remember to consider the nuances, particularly when dealing with decimal approximations of irrational numbers. Consistent practice with a range of examples will solidify your knowledge and allow you to tackle more advanced mathematical concepts with confidence. This comprehensive guide has equipped you with the necessary knowledge to confidently classify any number you encounter. Remember to continuously practice and explore to deepen your mathematical understanding.
Latest Posts
Latest Posts
-
How Many Liters Has In Half Gallon
Apr 03, 2025
-
What Is 20 Percent Of 150
Apr 03, 2025
-
Electrical Current Will Pass Easily Through
Apr 03, 2025
-
Which Of The Following Are Rational Numbers
Apr 03, 2025
-
Five Letter Words With Ie In Them
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Classify Each Number As Rational Or Irrational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
