What Is 20 Percent Of 150
Juapaving
Apr 03, 2025 · 4 min read
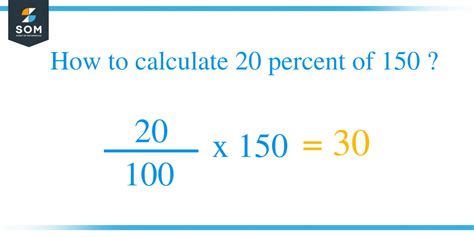
Table of Contents
What is 20 Percent of 150? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will thoroughly explore how to calculate 20 percent of 150, delve into the underlying principles of percentages, and illustrate their diverse applications in real-world scenarios. We'll also touch on advanced percentage calculations and problem-solving techniques.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 20 percent (20%) means 20 out of 100, or 20/100, which simplifies to 1/5.
Understanding this fundamental concept is crucial for grasping percentage calculations. The ability to convert between fractions, decimals, and percentages is essential for efficiently solving percentage problems.
Calculating 20 Percent of 150: The Simple Method
The most straightforward way to calculate 20 percent of 150 involves two simple steps:
-
Convert the percentage to a decimal: Divide the percentage by 100. In this case, 20% / 100 = 0.20
-
Multiply the decimal by the number: Multiply the decimal (0.20) by the number you want to find the percentage of (150). Therefore, 0.20 * 150 = 30
Therefore, 20 percent of 150 is 30.
Alternative Calculation Methods: Exploring Different Approaches
While the above method is the most efficient, let's explore alternative approaches to demonstrate a deeper understanding of percentage calculations:
Method 1: Using Fractions
As mentioned earlier, 20% is equivalent to the fraction 1/5. Therefore, to find 20% of 150, we can calculate (1/5) * 150. This simplifies to 150/5 = 30.
Method 2: Proportion Method
This method uses proportions to solve the problem. We can set up a proportion:
20/100 = x/150
Where 'x' represents the unknown value (20% of 150). Cross-multiplying, we get:
100x = 20 * 150
100x = 3000
x = 3000 / 100
x = 30
This confirms that 20% of 150 is 30.
Real-World Applications of Percentage Calculations
Percentage calculations are used extensively in various aspects of daily life and professional settings. Here are some examples:
-
Retail Discounts: Stores frequently offer discounts like "20% off." Knowing how to calculate percentages allows you to quickly determine the final price after the discount.
-
Sales Tax: Calculating sales tax on purchases involves determining a percentage of the total cost.
-
Tips and Gratuities: Calculating tips in restaurants often involves estimating a percentage of the bill amount.
-
Financial Investments: Tracking investment returns, calculating interest rates, and understanding stock market fluctuations all require percentage calculations.
-
Scientific Research: Percentages are used to represent data in experiments, surveys, and statistical analysis.
-
Data Analysis: Analyzing data sets, such as survey results or economic indicators, often involves calculating percentages to identify trends and patterns.
-
Grading Systems: Many educational systems use percentages to represent grades and scores.
Advanced Percentage Calculations and Problem Solving
Let's explore some more complex percentage problems:
Problem 1: Finding the Original Amount:
If 20% of a number is 30, what is the original number?
Solution: Let 'x' represent the original number. We can set up the equation:
0.20x = 30
x = 30 / 0.20
x = 150
Therefore, the original number is 150.
Problem 2: Calculating Percentage Increase or Decrease:
A product's price increased from $100 to $120. What is the percentage increase?
Solution: The increase is $120 - $100 = $20. To find the percentage increase, we divide the increase by the original price and multiply by 100:
($20 / $100) * 100 = 20%
Problem 3: Successive Percentage Changes:
A price is increased by 10% and then decreased by 10%. Is the final price the same as the original price?
Solution: No, the final price is not the same. Let's assume the original price is $100. A 10% increase results in $100 + ($100 * 0.10) = $110. A subsequent 10% decrease on $110 results in $110 - ($110 * 0.10) = $99. Therefore, the final price is less than the original price.
Utilizing Online Calculators and Tools
While understanding the principles of percentage calculations is crucial, various online calculators and tools can assist in performing quick calculations. These tools can be especially helpful when dealing with complex or repetitive calculations.
Conclusion
Calculating percentages is a fundamental mathematical skill with far-reaching applications. Understanding the different methods for calculating percentages, including using decimals, fractions, and proportions, allows for efficient and accurate problem-solving in diverse scenarios. Mastering percentage calculations empowers individuals to confidently navigate numerous aspects of their personal and professional lives, from managing finances to interpreting data and analyzing trends. While simple calculations like "What is 20 percent of 150?" are easily solvable, the underlying principles are fundamental to tackling more complex percentage problems and understanding their broad application across various fields.
Latest Posts
Latest Posts
-
What Is The Radius Of Circle With Centre N
Apr 04, 2025
-
Pick Up The Incorrect Statement From The Following
Apr 04, 2025
-
Fe Iron Rusts Physical Or Chemical Change
Apr 04, 2025
-
The Eye And Ear Are Part Of
Apr 04, 2025
-
Meiosis I And Meiosis Ii Different
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
