Can Scalene Triangles Be Right Triangles
Juapaving
Mar 28, 2025 · 5 min read
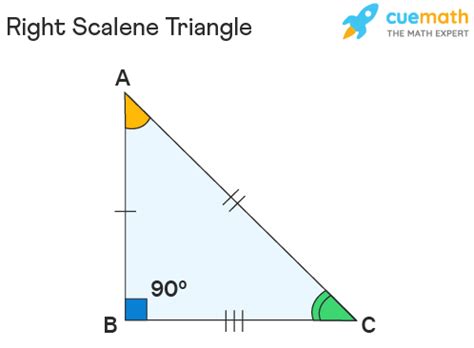
Table of Contents
Can Scalene Triangles Be Right Triangles? A Comprehensive Exploration
The question of whether scalene triangles can be right triangles is a fascinating one that delves into the fundamental properties of triangles. Understanding the definitions of both "scalene" and "right" triangles is crucial before we can definitively answer this question. This article will thoroughly explore this topic, providing a clear and comprehensive explanation supported by examples and visual aids. We'll also explore related concepts and common misconceptions to solidify your understanding.
Understanding the Definitions: Scalene and Right Triangles
Let's start by defining our key terms:
Scalene Triangle: A scalene triangle is a triangle where all three sides have different lengths. This means no two sides are equal in length. This unequal side length inherently dictates unequal angles as well.
Right Triangle: A right triangle is a triangle containing one right angle (a 90-degree angle). The side opposite the right angle is called the hypotenuse, and it is always the longest side of the right triangle. The other two sides are called legs or cathetus.
The critical point here is that these two definitions aren't mutually exclusive. A triangle can possess characteristics of both. The question then becomes, can a triangle simultaneously have three unequal sides and one 90-degree angle?
Exploring the Possibility: Can a Scalene Triangle Be a Right Triangle?
The short answer is a resounding yes. There is absolutely no inherent contradiction between being a scalene triangle and a right triangle. The properties that define each are independent of each other.
Consider the following example:
Imagine a right-angled triangle with sides of length 3, 4, and 5 units. This is a classic example of a Pythagorean triple, where the square of the hypotenuse (5²) is equal to the sum of the squares of the other two sides (3² + 4² = 9 + 16 = 25). Crucially, all three sides have different lengths. Therefore, this is a right triangle that is also a scalene triangle.
This demonstrates that the coexistence of these properties is not only possible but also readily demonstrable. Many other examples exist; the 3-4-5 triangle is just one of infinitely many possibilities. You could have a right triangle with sides of 5, 12, and 13, or countless other combinations where the sides are all different lengths and one angle is 90 degrees.
Visual Representation: Illustrating Scalene Right Triangles
Visualizing these concepts strengthens understanding. Imagine drawing a right-angled triangle. Now, carefully adjust the lengths of the two legs such that they are unequal. Notice that the hypotenuse will automatically adjust to maintain the right angle, and its length will be different from both legs. This simple exercise visually confirms the possibility of a scalene right triangle. This is easily accomplished with geometry software or even by hand drawing. The key is to ensure that you create a right angle and three sides of unequal length.
Common Misconceptions and Clarifications
A common misconception arises from the belief that if a triangle is scalene, it cannot be a right triangle. This misunderstanding stems from possibly focusing too much on the unequal sides and neglecting the possibility of one angle being 90 degrees. Remember that the definitions are independent; one does not preclude the other.
Another misconception is the assumption that all right triangles are isosceles (two sides of equal length). While isosceles right triangles do exist (with angles of 45-45-90), they are only a subset of all right triangles. The vast majority of right triangles are, in fact, scalene.
Mathematical Proof and the Pythagorean Theorem
The Pythagorean theorem further solidifies the possibility of scalene right triangles. The theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides (a² + b² = c², where 'c' is the hypotenuse). This theorem applies to all right triangles, including scalene ones. The crucial point is that the values of 'a' and 'b' can be any unequal positive numbers, thus creating an infinite set of scalene right triangles.
For example, if a = 6 and b = 8, then c² = 6² + 8² = 36 + 64 = 100, meaning c = 10. This is a scalene right triangle (sides 6, 8, and 10).
Expanding the Understanding: Beyond the Basics
The concept extends beyond simple numerical examples. Consider the application in more complex geometrical problems, such as those involving trigonometry. When solving problems involving right-angled triangles, recognizing the possibility of a scalene right triangle is essential for correctly applying the appropriate trigonometric functions (sine, cosine, tangent) and solving for unknown angles or side lengths.
Real-World Applications: Scalene Right Triangles in Practice
Scalene right triangles are prevalent in numerous real-world applications. They are found in:
- Engineering and Architecture: Designing structures, calculating slopes, and determining distances often involve scalene right triangles.
- Surveying and Mapping: Determining land boundaries and creating accurate maps frequently utilizes right-angled triangles with unequal sides.
- Computer Graphics and Game Development: Modeling three-dimensional objects and simulating realistic movement involves extensive use of vector mathematics, which relies heavily on right-angled triangles.
- Physics and Navigation: Calculating projectile trajectories, analyzing forces, and determining positions often utilize the principles of right triangles.
Conclusion: A Definitive Answer and its Implications
In conclusion, the answer to the question "Can scalene triangles be right triangles?" is a definitive yes. The properties of being scalene (having three unequal sides) and being a right triangle (having one 90-degree angle) are entirely compatible and often coexist. Understanding this fundamental concept is crucial for a strong grasp of geometry and its applications in various fields. This knowledge empowers you to approach geometric problems with greater confidence and accuracy. By understanding the independent nature of these definitions and the support offered by the Pythagorean theorem, we can confidently assert the existence and importance of scalene right triangles in both theoretical mathematics and real-world applications. The seemingly simple question reveals a deeper truth about the versatility and interconnectedness of geometric principles.
Latest Posts
Latest Posts
-
Two Angles Whose Measures Have A Sum Of 180
Mar 31, 2025
-
What Is 50 Centimeters In Inches
Mar 31, 2025
-
Instrument Used In Measuring Relative Humidity
Mar 31, 2025
-
Write The Chemical Formula For The Dichromate Ion
Mar 31, 2025
-
Step By Step Implicit Differentiation Calculator
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Can Scalene Triangles Be Right Triangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
