Altitude To The Base Of An Isosceles Triangle
Juapaving
Apr 01, 2025 · 5 min read
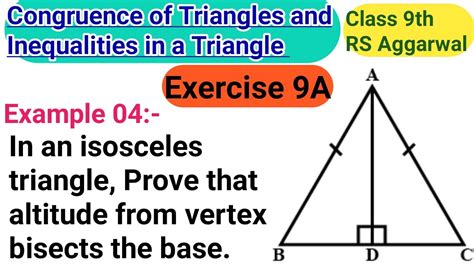
Table of Contents
Altitude to the Base of an Isosceles Triangle: A Comprehensive Guide
The altitude to the base of an isosceles triangle holds a special significance in geometry due to its unique properties and its role in solving various geometric problems. This article will delve deep into the characteristics of this altitude, exploring its relationship with other elements of the triangle, proving key theorems, and showcasing its applications in practical scenarios. We'll cover everything from basic definitions and theorems to advanced applications and problem-solving techniques.
Understanding Isosceles Triangles and Their Altitudes
An isosceles triangle is defined as a triangle with at least two sides of equal length. These equal sides are called the legs, and the third side is called the base. The angle formed by the two equal sides is called the vertex angle, while the angles opposite the legs are called the base angles. A crucial property of isosceles triangles is that their base angles are always equal.
The altitude of a triangle is a line segment drawn from a vertex perpendicular to the opposite side (or its extension). In the context of an isosceles triangle, the altitude drawn to the base holds particular importance. It possesses several unique properties that distinguish it from altitudes in other types of triangles.
Key Properties of the Altitude to the Base
-
Bisects the Base: The most significant property of the altitude to the base of an isosceles triangle is that it bisects the base. This means it divides the base into two equal segments. This property is a direct consequence of the symmetry inherent in isosceles triangles.
-
Bisects the Vertex Angle: The altitude to the base also bisects the vertex angle. This means it divides the angle formed by the two equal sides into two equal angles. This property further emphasizes the symmetry of the isosceles triangle.
-
Creates Two Congruent Right-Angled Triangles: The altitude to the base divides the isosceles triangle into two congruent right-angled triangles. This congruence is a powerful tool for solving problems involving the sides and angles of the isosceles triangle. The congruence can be proved using the Side-Angle-Side (SAS) congruence postulate.
-
Median and Angle Bisector: The altitude to the base of an isosceles triangle also acts as both the median (a line segment from a vertex to the midpoint of the opposite side) and the angle bisector (a line segment that divides an angle into two equal angles) of the base. This triple role (altitude, median, and angle bisector) is unique to the altitude to the base in an isosceles triangle.
Proving the Key Properties
Let's rigorously prove the two most important properties mentioned above: the altitude bisecting the base and bisecting the vertex angle.
Proof 1: Altitude bisects the base
Consider an isosceles triangle ABC, where AB = AC. Let AD be the altitude drawn from A to the base BC. We want to prove that BD = DC.
We can use the Right Angle-Hypotenuse-Side (RHS) congruence rule. In right-angled triangles ABD and ACD:
- AB = AC (given)
- AD = AD (common side)
- ∠ADB = ∠ADC = 90° (AD is the altitude)
Therefore, by RHS congruence, ΔABD ≅ ΔACD. Consequently, BD = DC. Hence, the altitude AD bisects the base BC.
Proof 2: Altitude bisects the vertex angle
Using the same isosceles triangle ABC and altitude AD, we want to prove that ∠BAD = ∠CAD.
Since ΔABD ≅ ΔACD (proven above), we know that corresponding angles are equal. Therefore, ∠BAD = ∠CAD. This proves that the altitude AD bisects the vertex angle ∠BAC.
Applications and Problem Solving
The properties of the altitude to the base of an isosceles triangle are frequently used to solve various geometric problems. Let's explore some examples:
Example 1: Finding the Length of the Altitude
Given an isosceles triangle with legs of length 10 cm and a base of length 12 cm, find the length of the altitude to the base.
The altitude bisects the base, creating two right-angled triangles with hypotenuse 10 cm and one leg 6 cm (half of the base). Using the Pythagorean theorem:
Altitude² + 6² = 10² Altitude² = 100 - 36 = 64 Altitude = 8 cm
Example 2: Finding the Area of an Isosceles Triangle
Given an isosceles triangle with legs of length 13 cm and a base of length 10 cm, find the area of the triangle.
First, find the altitude using the Pythagorean theorem as shown in Example 1. Then, calculate the area using the formula: Area = (1/2) * base * altitude.
Example 3: Solving Problems involving Angles
Knowing that the altitude bisects the vertex angle allows us to solve problems involving the angles of the isosceles triangle. If the vertex angle is given, we can easily find the base angles (which are equal) and vice-versa.
Advanced Applications and Extensions
The concepts related to the altitude to the base extend to more advanced geometric topics:
-
Coordinate Geometry: The altitude can be used to find the coordinates of the vertices and other important points in an isosceles triangle defined on a Cartesian plane.
-
Trigonometry: Trigonometric functions can be used to find the length of the altitude and other sides of the triangle if certain angles and sides are known.
-
Three-Dimensional Geometry: Similar concepts apply to isosceles triangles embedded in three-dimensional spaces.
Conclusion
The altitude to the base of an isosceles triangle is a fundamental concept in geometry with far-reaching applications. Its unique properties – bisecting both the base and the vertex angle, creating congruent right-angled triangles, and serving as both median and angle bisector – make it a crucial tool for solving numerous geometric problems. Understanding these properties and their proofs provides a solid foundation for tackling more complex geometric challenges. From basic area calculations to advanced coordinate geometry applications, the altitude remains a cornerstone in the study of isosceles triangles. Mastering its properties is essential for anyone seeking a deep understanding of geometry.
Latest Posts
Latest Posts
-
What Does The Fine Adjustment Knob Do On A Microscope
Apr 02, 2025
-
How Many Valence Electrons In Helium
Apr 02, 2025
-
An Equilateral Triangle Has Three Equal Angles
Apr 02, 2025
-
Labelled Diagram Of Male Reproductive Organ
Apr 02, 2025
-
How Many Cm Is 6 4
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Altitude To The Base Of An Isosceles Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
