Find The Square Root Of 121
Juapaving
Apr 02, 2025 · 5 min read
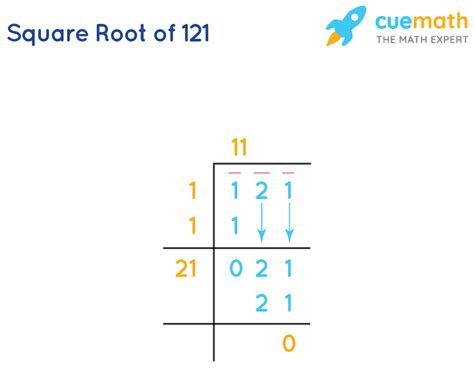
Table of Contents
- Find The Square Root Of 121
- Table of Contents
- Finding the Square Root of 121: A Comprehensive Guide
- What is a Square Root?
- Method 1: Direct Calculation (Mental Math)
- Method 2: Prime Factorization
- Method 3: Using a Calculator
- Method 4: Newton's Method (Iterative Approach)
- Understanding Perfect Squares
- Historical Context: The Evolution of Square Roots
- Applications of Square Roots
- Conclusion: Beyond the Simple Answer
- Latest Posts
- Latest Posts
- Related Post
Finding the Square Root of 121: A Comprehensive Guide
Finding the square root of 121 might seem like a simple task, especially for those familiar with basic arithmetic. However, understanding the underlying concepts and exploring different methods to solve this problem can lead to a deeper appreciation of mathematics and its applications. This comprehensive guide will delve into various approaches to finding the square root of 121, catering to different levels of mathematical understanding. We'll explore the fundamental principles, examine practical techniques, and even touch upon the historical context surrounding square roots.
What is a Square Root?
Before diving into the specifics of finding the square root of 121, let's establish a clear understanding of what a square root actually represents. In simple terms, the square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. This relationship is often represented mathematically as:
√x = y if and only if y² = x
Where 'x' is the number and 'y' is its square root. The symbol '√' is known as the radical symbol.
Method 1: Direct Calculation (Mental Math)
For smaller, perfect squares like 121, the most straightforward approach is simply knowing the multiplication table. If you're familiar with your times tables, you’ll recognize that 11 multiplied by itself (11²) equals 121. Therefore, the square root of 121 is 11.
This method relies on memorization and is efficient for numbers with easily recognizable square roots. However, this method becomes less practical for larger numbers.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the square root of numbers, especially perfect squares. It involves breaking down the number into its prime factors—numbers divisible only by 1 and themselves.
Let's apply this method to 121:
-
Find the prime factors of 121: 121 is divisible by 11 (11 x 11 = 121). Since 11 is a prime number, the prime factorization of 121 is 11 x 11 or 11².
-
Pair up the prime factors: Notice that we have two 11s. This pairing is crucial.
-
Calculate the square root: Take one factor from each pair. In this case, we have one 11. Therefore, the square root of 121 is 11.
This method is helpful for understanding the structure of perfect squares and can be applied to larger numbers, though it might be more time-consuming for very large numbers.
Method 3: Using a Calculator
For larger numbers or when speed is essential, using a calculator is the most efficient method. Most calculators have a dedicated square root function (usually denoted as √). Simply enter 121 and press the square root button; the calculator will instantly return the answer: 11.
Calculators are invaluable tools for handling complex calculations, making them especially useful for numbers with non-integer square roots (such as the square root of 2, which is an irrational number).
Method 4: Newton's Method (Iterative Approach)
Newton's method is a numerical technique used to approximate the square root of a number. It’s an iterative process, meaning it refines the approximation with each step, getting closer to the actual value. While overkill for finding the square root of 121, it's a valuable method for understanding iterative numerical techniques in mathematics. The formula for Newton's method for finding the square root of 'x' is:
x_(n+1) = 0.5 * (x_n + x/x_n)
Where:
- x_n is the current approximation
- x_(n+1) is the next, improved approximation
- x is the number whose square root is sought (121 in our case)
Let's illustrate this with a few iterations:
-
Initial Guess: Let's start with an initial guess of x_0 = 10.
-
Iteration 1: x_1 = 0.5 * (10 + 121/10) = 11.05
-
Iteration 2: x_2 = 0.5 * (11.05 + 121/11.05) ≈ 11.0002
As you can see, after just a couple of iterations, we're already very close to the actual square root (11). Newton's method demonstrates the power of iterative algorithms for solving mathematical problems.
Understanding Perfect Squares
The number 121 is a perfect square because it's the product of an integer multiplied by itself (11 x 11). Understanding perfect squares is crucial for working with square roots. Other examples of perfect squares include:
- 1 (1 x 1)
- 4 (2 x 2)
- 9 (3 x 3)
- 16 (4 x 4)
- 25 (5 x 5)
- and so on...
Recognizing perfect squares can significantly simplify calculations involving square roots.
Historical Context: The Evolution of Square Roots
The concept of square roots has a rich history, tracing back to ancient civilizations. The Babylonians, as early as 1800 BC, developed methods for approximating square roots. The Greeks also made significant contributions, with mathematicians like Euclid exploring geometric approaches to understanding square roots. Over time, mathematical understanding evolved, leading to the development of sophisticated algorithms and computational methods for calculating square roots.
Applications of Square Roots
Square roots aren't just abstract mathematical concepts; they have practical applications across various fields:
- Physics: Calculating distances, velocities, and accelerations often involves using square roots.
- Engineering: Designing structures and calculating forces frequently requires the use of square roots.
- Computer Graphics: Generating images and animations often relies on square root calculations.
- Finance: Calculating investment returns and risk assessments may involve square roots.
- Statistics: Statistical analysis uses square roots in various calculations, including standard deviation.
Conclusion: Beyond the Simple Answer
While the answer to "find the square root of 121" is simply 11, this exploration goes beyond a simple calculation. It demonstrates the richness of mathematical concepts, introduces various solution methods, and highlights the historical and practical significance of square roots. Whether using mental math, prime factorization, a calculator, or even an iterative approach like Newton's method, understanding the underlying principles is crucial for mastering mathematical concepts and applying them to real-world problems. The journey of finding the square root of 121 serves as a microcosm of the broader mathematical landscape, showcasing the elegance and power of mathematics.
Latest Posts
Latest Posts
-
Are Rational Numbers Closed Under Multiplication
Apr 07, 2025
-
Least Common Multiple Of 5 And 25
Apr 07, 2025
-
How Many Resonance Structures Does So3 Have
Apr 07, 2025
-
Which Of The Following Is The Strongest Acid
Apr 07, 2025
-
Which Of The Following Is Not A Connective Tissue
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Find The Square Root Of 121 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
