Finding Area Under A Curve Calculator
Juapaving
Apr 01, 2025 · 5 min read
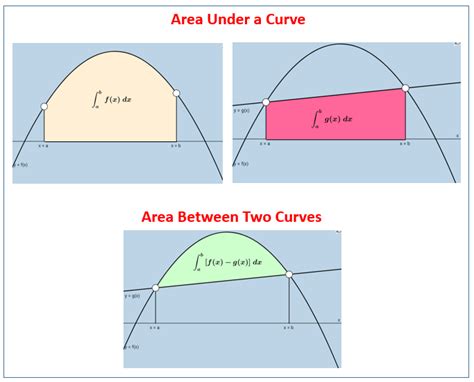
Table of Contents
Finding the Area Under a Curve Calculator: A Comprehensive Guide
Finding the area under a curve is a fundamental concept in calculus with widespread applications across various fields like physics, engineering, economics, and statistics. Manually calculating this area can be complex and time-consuming, especially for intricate functions. This is where a finding the area under a curve calculator becomes invaluable. This comprehensive guide explores the concept, its applications, the different methods used in calculators, and how to effectively utilize these tools.
Understanding the Area Under a Curve
The area under a curve represents the integral of a function over a specified interval. Geometrically, it's the area bounded by the curve, the x-axis, and two vertical lines representing the limits of integration. For a positive function, this area is always positive. For functions that dip below the x-axis, the area below the axis is considered negative. The total signed area accounts for both positive and negative areas.
Why is Finding the Area Under a Curve Important?
The applications are numerous and far-reaching:
- Physics: Calculating displacement from velocity, work from force, and other physical quantities.
- Engineering: Determining the center of gravity, calculating fluid flow, and analyzing stress and strain.
- Economics: Computing total cost, revenue, or profit over a period.
- Statistics: Finding probabilities using probability density functions.
- Computer Science: Approximating integrals in simulations and algorithms.
Methods for Calculating the Area Under a Curve
While there are analytical methods for finding exact areas under curves (using integration techniques), many functions don't have readily available antiderivatives. This is where numerical methods implemented in calculators become essential. These calculators typically employ several techniques:
1. Riemann Sums
This is a fundamental numerical integration technique that approximates the area using rectangles. Different variations exist:
- Left Riemann Sum: Uses the left endpoint of each subinterval to determine the rectangle's height.
- Right Riemann Sum: Uses the right endpoint.
- Midpoint Riemann Sum: Uses the midpoint of each subinterval.
- Trapezoidal Rule: Approximates the area using trapezoids instead of rectangles, generally providing a more accurate approximation.
The accuracy of Riemann sums improves as the number of subintervals (rectangles or trapezoids) increases. Calculators often allow you to specify the number of subintervals for better control over precision.
2. Simpson's Rule
This method uses quadratic polynomials to approximate the curve within each subinterval, yielding a more accurate result than the trapezoidal rule for the same number of subintervals. It's particularly effective for smoother curves.
3. Monte Carlo Integration
This probabilistic method utilizes random sampling to estimate the area. Points are randomly generated within a bounding rectangle containing the curve. The ratio of points falling under the curve to the total number of points provides an estimate of the area. While less efficient than other methods for smooth functions, Monte Carlo integration excels with high-dimensional integrals and complex shapes.
4. Adaptive Quadrature
This sophisticated technique adjusts the number of subintervals in different parts of the integration range. It focuses on areas where the function is changing rapidly, improving accuracy and efficiency. Adaptive quadrature is often the default method in advanced calculators because it automatically adapts to the curve's complexity.
Using a Finding the Area Under a Curve Calculator
The specific steps involved vary depending on the calculator, but generally include:
-
Inputting the Function: Enter the mathematical expression defining the curve accurately. Most calculators accept standard mathematical notation.
-
Specifying the Integration Limits: Provide the lower and upper bounds of the interval for which you want to calculate the area.
-
Selecting the Method (Optional): Some calculators allow you to choose the numerical integration method (Riemann sum, trapezoidal rule, Simpson's rule, etc.). If not specified, the calculator may use a default method like adaptive quadrature.
-
Specifying the Number of Subintervals (Optional): For Riemann sums and other methods, you might be able to set the number of subintervals. Higher numbers generally lead to increased accuracy but also longer computation times.
-
Calculating the Area: Once the input is provided, the calculator computes the area under the curve. The result is displayed with a certain level of precision.
Choosing the Right Calculator
The best calculator for finding the area under a curve depends on your needs and the complexity of the problem:
-
Simple Online Calculators: Suitable for basic functions and quick calculations. These often use simple numerical integration methods.
-
Scientific Calculators: Provide more advanced features, including a wider range of integration methods and higher precision.
-
Mathematical Software Packages (e.g., Mathematica, Maple, MATLAB): Offer the most powerful tools for complex functions and high accuracy. These packages often incorporate symbolic integration capabilities as well as sophisticated numerical methods.
Advanced Applications and Considerations
Beyond basic area calculations, finding the area under a curve calculators can handle more sophisticated problems:
-
Improper Integrals: These integrals extend to infinity or have singularities within the integration range. Specialized techniques are needed for these, and some calculators can handle them directly.
-
Double and Triple Integrals: Calculators can often compute areas in higher dimensions.
-
Integration with Respect to Different Variables: You can find areas under curves defined by functions involving multiple variables.
-
Error Analysis: Understanding the inherent error in numerical integration is crucial. Calculators may provide estimates of the error, which helps assess the reliability of the results.
Tips for Effective Use
-
Check Your Input: Double-check your function and integration limits to avoid errors.
-
Experiment with Methods: If you have the option, try different numerical integration methods to compare results.
-
Increase Subintervals (if needed): For greater accuracy, increase the number of subintervals, especially for complex functions.
-
Understand Limitations: Numerical methods provide approximations, not exact solutions. Be aware of the limitations and potential error sources.
-
Visualize Results: Whenever possible, use the calculator's visualization tools to see the graphical representation of the area under the curve.
Conclusion
Finding the area under a curve is a fundamental task with far-reaching implications. While analytical methods provide exact results for certain functions, numerical methods implemented in calculators are essential for many practical scenarios. By understanding the different methods available and the capabilities of various calculators, you can effectively leverage these tools to solve diverse problems in various fields, from physics and engineering to economics and statistics. Choosing the right calculator and understanding its capabilities is crucial for obtaining reliable and accurate results. The proper application of these tools empowers you to tackle complex mathematical challenges with efficiency and precision. Remember to always double-check your input and analyze the results critically to ensure accuracy and relevance to your specific problem.
Latest Posts
Latest Posts
-
Why Does Fluorine Have A Higher Ionization Energy Than Iodine
Apr 02, 2025
-
5 Letter Words Start With A D
Apr 02, 2025
-
What Is The Smallest Particle Of An Element
Apr 02, 2025
-
Electron Microscope Advantages Over Light Microscope
Apr 02, 2025
-
Hc Verma Part 1 Table Of Contents
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Finding Area Under A Curve Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
