How To Find The Latus Rectum Of A Parabola
Juapaving
Mar 30, 2025 · 6 min read
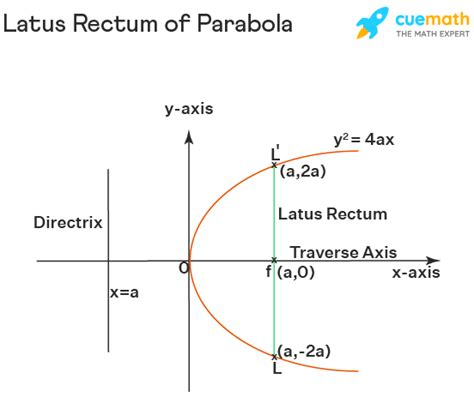
Table of Contents
How to Find the Latus Rectum of a Parabola: A Comprehensive Guide
The latus rectum of a parabola is a crucial component in understanding its shape and properties. This comprehensive guide will delve deep into the concept of the latus rectum, explaining its definition, various methods for calculating its length, and its significance in different forms of parabolic equations. We'll cover everything from the standard equation to more complex cases, ensuring you gain a thorough understanding of this essential element of conic sections.
Understanding the Latus Rectum
The latus rectum of a parabola is a line segment that passes through the focus of the parabola and is parallel to the directrix. It's perpendicular to the axis of symmetry and has its endpoints on the parabola. Think of it as the width of the parabola at its focus. Its length is directly related to the parabola's focal length (the distance between the focus and the vertex). Understanding the latus rectum allows for a more complete comprehension of the parabola's geometry and its various applications.
Key Characteristics:
- Passes through the focus: One end of the latus rectum always lies on the focus.
- Parallel to the directrix: The line segment is parallel to the directrix of the parabola.
- Perpendicular to the axis of symmetry: The latus rectum is always perpendicular to the parabola's axis of symmetry.
- Endpoints on the parabola: Both endpoints of the latus rectum lie on the curve of the parabola.
Calculating the Length of the Latus Rectum
The length of the latus rectum is directly proportional to the parabola's focal length. The formula for calculating the length is remarkably consistent across various forms of the parabolic equation.
The Universal Formula:
The length of the latus rectum, often denoted as 4p, is always four times the absolute value of the focal length (p). This holds true regardless of whether the parabola opens upwards, downwards, leftwards, or rightwards. The focal length (p) is the distance from the vertex to the focus.
|p| = |focal length|
Therefore, Length of Latus Rectum = 4|p|
This simple formula provides a universal method for determining the latus rectum's length, independent of the orientation or specific form of the parabola's equation.
Finding the Latus Rectum in Different Forms of Parabola Equations
Parabolas can be represented in various forms. Let's explore how to find the latus rectum in each case:
1. Standard Form: (x - h)² = 4p(y - k) and (y - k)² = 4p(x - h)
These are the most common representations of parabolas, where (h, k) represents the vertex.
-
(x - h)² = 4p(y - k): This represents a parabola opening upwards (if p > 0) or downwards (if p < 0). The value of
pdirectly gives the focal length. The length of the latus rectum is4|p|. -
(y - k)² = 4p(x - h): This represents a parabola opening rightwards (if p > 0) or leftwards (if p < 0). Again, the value of
prepresents the focal length, and the length of the latus rectum is4|p|.
Example:
Find the length of the latus rectum for the parabola (x - 2)² = 8(y + 1).
Here, 4p = 8, so p = 2. The length of the latus rectum is 4|p| = 4(2) = 8.
2. General Form: Ax² + Bxy + Cy² + Dx + Ey + F = 0
The general form can be more complex, but we can still extract the necessary information. The process involves completing the square to transform the equation into the standard form and then determine the value of p. This requires a thorough understanding of conic section transformations.
Steps:
- Group x and y terms: Separate the x and y terms and group them accordingly.
- Complete the square: Complete the square for both x and y terms to obtain a perfect square trinomial.
- Rewrite in standard form: Rewrite the equation in either (x - h)² = 4p(y - k) or (y - k)² = 4p(x - h) form.
- Determine p: Identify the value of
pfrom the standard form. - Calculate the latus rectum: Use the formula
4|p|to find the length of the latus rectum.
This method can be quite involved and requires strong algebraic manipulation skills.
3. Using the Focus and Directrix
The definition itself provides a method. If you know the coordinates of the focus and the equation of the directrix, you can calculate the focal length and subsequently the latus rectum.
The focal length (p) is the perpendicular distance between the focus and the directrix. Once you have p, use the formula 4|p| to obtain the latus rectum length.
Example:
A parabola has a focus at (2, 3) and a directrix of y = 1. The distance between the focus and the directrix is |3 - 1| = 2, so p = 2. The length of the latus rectum is 4|2| = 8.
4. Using the Vertex and Focus
Knowing the coordinates of both the vertex and the focus allows for easy calculation of the focal length.
The distance between the vertex and the focus is the focal length (p). Once you have p, the length of the latus rectum is again 4|p|.
Significance of the Latus Rectum
The latus rectum holds significant importance in understanding and analyzing parabolas:
- Shape and Width: It determines the width of the parabola at its focus, giving an indication of its overall shape and spread.
- Reflection Properties: In optical and radio telescopes, parabolic reflectors utilize the latus rectum's properties to focus incoming parallel rays at the focus. The latus rectum plays a key role in understanding the effectiveness of such reflectors.
- Geometric Properties: The latus rectum is integral to several geometrical properties of the parabola, including determining tangents and chords.
- Equation Derivation: The latus rectum is a key component in deriving the standard equation of a parabola from its focus and directrix.
Advanced Applications and Considerations
The concept of the latus rectum extends to more complex scenarios.
- Rotated Parabolas: Even when the parabola is rotated, the fundamental principles remain. The calculations might involve more advanced techniques like matrix transformations, but the length of the latus rectum remains
4|p|. - Parametric Equations: When parabolas are represented using parametric equations, finding the latus rectum may involve implicit differentiation and other advanced calculus techniques.
- Three-Dimensional Paraboloids: The concept can be extended to three dimensions, where paraboloids have a latus rectum that forms an ellipse.
Conclusion
Finding the latus rectum of a parabola is a fundamental skill in understanding this important conic section. While the basic formula 4|p| is remarkably consistent, various approaches exist depending on the form of the parabolic equation and available information. This comprehensive guide equips you with the knowledge and techniques to confidently determine the latus rectum in different scenarios, strengthening your understanding of parabolic geometry and its applications. Remember to always visualize the parabola's shape and orientation to ensure accurate calculations and interpretations.
Latest Posts
Latest Posts
-
Butter Melting Is A Physical Change
Apr 01, 2025
-
Lowest Common Multiple Of 20 And 8
Apr 01, 2025
-
A Mixture Can Be Made Up Of Two Or More
Apr 01, 2025
-
Common Denominator For 3 And 4
Apr 01, 2025
-
How To Spell 20 In Word Form
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Latus Rectum Of A Parabola . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
