Which Graph Has A Slope Of 4/5
Juapaving
Apr 04, 2025 · 6 min read
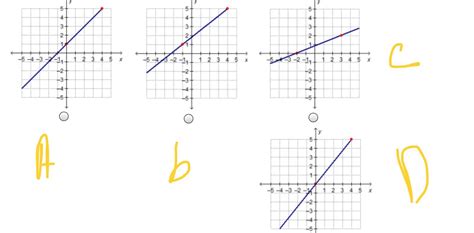
Table of Contents
Which Graph Has a Slope of 4/5? A Comprehensive Guide
Understanding slope is fundamental to grasping linear relationships in mathematics and across various fields. This comprehensive guide delves into the concept of slope, specifically focusing on identifying graphs with a slope of 4/5. We'll explore different methods for determining slope, practical applications, and common misconceptions. By the end, you'll confidently identify graphs showcasing this specific slope.
Understanding Slope: The Foundation
The slope of a line represents its steepness or incline. It's defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on the line. Mathematically, the slope (often denoted as 'm') is calculated as:
m = (y₂ - y₁) / (x₂ - x₁)
Where (x₁, y₁) and (x₂, y₂) are any two points on the line. A positive slope indicates an upward trend from left to right, while a negative slope shows a downward trend. A slope of zero means the line is horizontal, and an undefined slope signifies a vertical line.
Identifying a Slope of 4/5: Visual Clues
A slope of 4/5 means that for every 5 units moved horizontally (run), the line rises 4 units vertically (rise). This ratio is consistent across all points on the line. When visually inspecting a graph, look for these key characteristics:
1. Positive and Gentle Incline:
A slope of 4/5 is positive, indicating an upward trend from left to right. Importantly, it's a relatively gentle incline. It's not as steep as a slope of, say, 2 or 3, but steeper than a slope of 1/2 or 1/5.
2. Rise over Run:
Carefully observe the movement between two clearly marked points on the line. Measure the vertical distance (rise) and the horizontal distance (run) between these points. If the ratio of rise to run consistently equals 4/5 (or an equivalent fraction like 8/10 or 12/15), then the line possesses the desired slope.
3. Using Gridlines:
Graphs with clearly marked gridlines simplify slope identification. Start at a point where the line intersects a grid intersection. Count the units upwards (rise) and then rightwards (run) to reach another grid intersection on the line. The ratio should be 4/5. You can also work backwards – count 4 units down and 5 units left to find another point on the line.
Mathematical Methods for Verification
While visual inspection offers a quick estimate, precise verification requires mathematical calculations.
1. Selecting Two Points:
Choose any two clearly identifiable points on the graph where the coordinates (x, y) can be determined. The accuracy of your slope calculation directly depends on the accuracy of these point selections. Avoid estimating points; choose points that clearly intersect grid lines or are precisely defined.
2. Applying the Slope Formula:
Substitute the coordinates of the selected points into the slope formula: m = (y₂ - y₁) / (x₂ - x₁). The result should equal 4/5 or an equivalent fraction like 0.8.
3. Multiple Point Verification:
To enhance accuracy and confirm consistency, repeat steps 1 and 2 with different pairs of points on the same line. If the slope remains consistently 4/5, you can confidently conclude that the graph indeed represents a line with that specific slope.
Real-World Applications of Slope: Beyond the Classroom
The concept of slope transcends theoretical mathematics, finding practical applications in numerous fields:
1. Engineering and Construction:
Slope calculations are crucial in civil engineering for designing roads, ramps, and other infrastructure. A specific slope is often required to ensure safety, functionality, and compliance with building codes. For example, the slope of a wheelchair ramp needs to be carefully calculated for accessibility.
2. Finance and Economics:
In finance, slope is used to analyze trends in stock prices, investment returns, and economic indicators. A positive slope indicates growth, while a negative slope signals decline. The steepness of the slope indicates the rate of change.
3. Physics and Science:
Slope is fundamental in physics for understanding concepts like velocity (slope of a distance-time graph) and acceleration (slope of a velocity-time graph). It's also employed in various scientific fields to analyze experimental data and model relationships between variables.
4. Data Analysis and Machine Learning:
In data science and machine learning, linear regression, a statistical method that finds the best-fitting line through data points, relies heavily on the concept of slope. The slope of the regression line provides insights into the relationship between the variables being analyzed.
Common Misconceptions about Slope
Several misconceptions can lead to inaccurate slope interpretation:
1. Ignoring the Scale:
Incorrectly interpreting the scale of the graph axes is a common mistake. Always ensure you are accurately reading the units on both the x-axis and y-axis before calculating the slope.
2. Reversing Rise and Run:
Confusing the rise and run in the slope calculation is a frequent error. Remember, rise is the vertical change, and run is the horizontal change.
3. Focusing on a Single Point:
Slope is a property of the entire line, not a single point. Analyzing the slope at a single point is meaningless; you need to consider the change between two points.
4. Assuming Linearity:
The slope calculation only applies to linear relationships. If the graph is curved or nonlinear, the slope will vary across different points on the curve.
Advanced Considerations: Slope and Linear Equations
The slope of a line is intimately linked to its equation. The standard form of a linear equation is:
y = mx + c
where 'm' is the slope, and 'c' is the y-intercept (the point where the line crosses the y-axis). Knowing the slope (m = 4/5) allows us to partially define the equation of the line. To fully determine the equation, we need at least one point on the line to find the value of 'c'.
For example, if a line with a slope of 4/5 passes through the point (5, 4), we can substitute these values into the equation:
4 = (4/5)*5 + c
Solving for 'c', we find c = 0. Therefore, the equation of this line is y = (4/5)x.
Conclusion: Mastering Slope Identification
Identifying graphs with a specific slope like 4/5 requires a combination of visual inspection, careful mathematical calculations, and a solid understanding of the underlying principles. By following the methods outlined in this guide, and by avoiding common pitfalls, you can accurately determine whether a given graph displays the desired slope. Remembering that slope represents a consistent rate of change throughout the line is critical. This understanding will not only improve your mathematical skills but also equip you to tackle real-world problems where slope plays a vital role.
Latest Posts
Latest Posts
-
Anaerobic Respiration Takes Place In The
Apr 05, 2025
-
Can Dielectric Constant Be Less Than 1
Apr 05, 2025
-
1 1 4 As A Percent
Apr 05, 2025
-
Where In The Cell Does Krebs Cycle Occur
Apr 05, 2025
-
A Man Standing On The Roof Of A House
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Which Graph Has A Slope Of 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
