1 1 4 As A Percent
Juapaving
Apr 05, 2025 · 5 min read
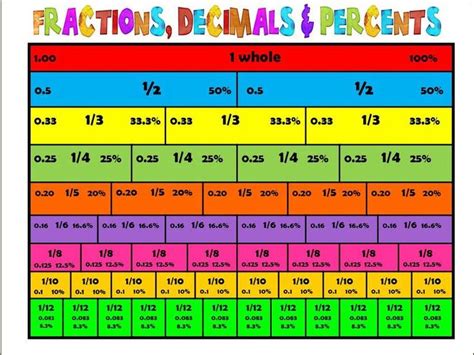
Table of Contents
1 1/4 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and tips to understanding financial reports and statistical data. This article delves into the conversion of the mixed number 1 1/4 into a percentage, exploring the process step-by-step and providing various practical examples to solidify your understanding.
Understanding the Basics: Fractions, Decimals, and Percentages
Before we tackle the conversion of 1 1/4 to a percentage, let's briefly review the relationships between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Express a part of a whole as a ratio of two numbers (numerator/denominator). For example, 1/4 represents one part out of four equal parts.
-
Decimals: Express a part of a whole as a number with a decimal point. Decimals are based on powers of 10. For example, 0.25 is equivalent to 25/100.
-
Percentages: Express a part of a whole as a number out of 100. The symbol "%" represents "per cent" or "out of 100". For example, 25% means 25 out of 100.
These three forms are interchangeable. Understanding their relationship is crucial for performing various mathematical operations.
Converting 1 1/4 to a Percentage: A Step-by-Step Guide
The mixed number 1 1/4 represents one whole unit plus one-quarter of a unit. To convert this to a percentage, we follow these steps:
Step 1: Convert the Mixed Number to an Improper Fraction
A mixed number combines a whole number and a fraction. To make the conversion easier, we first change the mixed number 1 1/4 into an improper fraction. This involves multiplying the whole number (1) by the denominator (4) and adding the numerator (1). The result becomes the new numerator, while the denominator remains the same.
1 1/4 = (1 * 4 + 1) / 4 = 5/4
Step 2: Convert the Improper Fraction to a Decimal
Next, we convert the improper fraction 5/4 into a decimal by dividing the numerator (5) by the denominator (4):
5 ÷ 4 = 1.25
Step 3: Convert the Decimal to a Percentage
Finally, we convert the decimal 1.25 to a percentage by multiplying it by 100 and adding the percentage symbol (%):
1.25 * 100 = 125%
Therefore, 1 1/4 is equivalent to 125%.
Understanding the Meaning of 125%
A percentage greater than 100% indicates that the value exceeds the whole. In this case, 125% means 125 parts out of 100, or one and a quarter times the original whole. This is a crucial concept to grasp, especially when dealing with percentage increases, growth rates, or situations where values exceed the base amount.
Practical Applications of Converting 1 1/4 to a Percentage
The conversion of 1 1/4 to 125% has numerous practical applications in various fields:
1. Percentage Increases and Growth
Imagine a company's profit increased by 1 1/4 times its previous year's profit. This represents a 125% increase. This information is vital for analyzing business performance and forecasting future growth. Understanding percentage increases and decreases is crucial for financial planning, investment analysis, and business decision-making.
2. Calculating Discounts and Markups
Retailers often offer discounts or mark up prices by a certain percentage. For example, if a store advertises a 125% markup on a product, it means the selling price is 1.25 times the original cost price. Conversely, a 25% discount means the price is 75% (100% - 25%) of the original cost.
3. Statistical Analysis and Data Interpretation
Percentages are frequently used to represent data in statistics. For instance, if a survey shows that 125% of the projected responses have been received, it indicates that more responses were received than initially anticipated. This requires careful consideration of the context and data collection methods.
4. Financial Calculations
Percentage calculations are essential in various financial applications, including calculating interest rates, compound interest, returns on investments, and loan repayments. For example, calculating interest accrued over a period might involve multiplying the principal amount by 125% to find the total amount after accounting for the interest.
5. Scientific and Engineering Calculations
In scientific and engineering fields, percentages are often used to express ratios, proportions, and changes in quantities. For example, expressing the efficiency of a machine or the increase in a chemical reaction might involve calculations using percentages, which ultimately rely on the conversion and understanding of fractions and decimals.
Alternative Methods for Converting 1 1/4 to a Percentage
While the step-by-step method outlined above is straightforward, other methods can achieve the same result.
Method 1: Using Proportions
We can set up a proportion to solve for the percentage:
x/100 = 1 1/4/1
Solving for x will yield the percentage equivalent of 1 1/4.
Method 2: Using a Calculator
Most calculators can directly handle fraction-to-decimal and decimal-to-percentage conversions. Simply enter 1 1/4 (as 5/4 or 1.25) and use the percentage function to obtain the result.
Common Mistakes to Avoid When Converting Fractions to Percentages
Several common errors can occur when converting fractions to percentages. Understanding these pitfalls can prevent inaccuracies in your calculations:
-
Incorrect conversion of mixed numbers to improper fractions: Ensure that you accurately multiply the whole number by the denominator and add the numerator before dividing by the denominator.
-
Errors in decimal division: Double-check your calculations when dividing the numerator by the denominator to prevent errors in the decimal representation.
-
Forgetting to multiply by 100: Remember that the final step involves multiplying the decimal by 100 to obtain the percentage.
-
Misinterpreting percentages over 100%: Remember that a percentage exceeding 100% indicates a value greater than the whole.
Conclusion: Mastering Percentage Conversions
Converting 1 1/4 to a percentage (125%) is a simple yet important mathematical skill with broad applications. Mastering this conversion requires a solid understanding of fractions, decimals, and the concept of percentages. This knowledge is crucial for various real-world applications, from everyday financial transactions to complex scientific calculations. By carefully following the steps outlined above and avoiding common pitfalls, you can confidently handle percentage conversions and apply this essential skill in diverse contexts. Remember to practice regularly to reinforce your understanding and improve your speed and accuracy. The ability to effortlessly convert between fractions, decimals, and percentages is an invaluable asset in navigating the numerical world around us.
Latest Posts
Latest Posts
-
What Is Xx11 In Roman Numerals
Apr 05, 2025
-
What Is A Shape Called With 11 Sides
Apr 05, 2025
-
Least Common Multiple Of 4 And 11
Apr 05, 2025
-
Abiotic Factor Affecting A Biotic Factor
Apr 05, 2025
-
5 Letter Words Starting With Pra
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about 1 1 4 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
