Where Is The Circumcenter Of A Right Triangle Located
Juapaving
Mar 30, 2025 · 5 min read
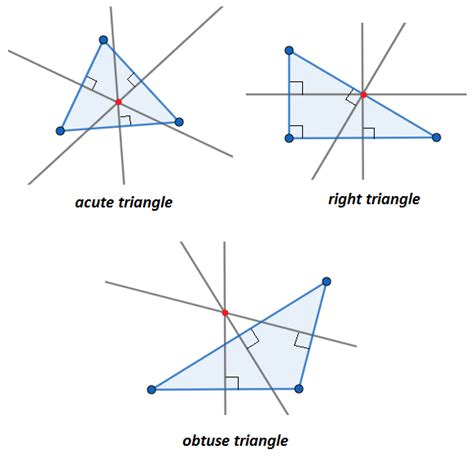
Table of Contents
Where is the Circumcenter of a Right Triangle Located? A Comprehensive Guide
The circumcenter of any triangle, including a right-angled triangle, holds a unique and fascinating geometric property. Understanding its location is key to grasping fundamental concepts in geometry and trigonometry. This comprehensive guide will delve deep into the specifics of locating the circumcenter of a right triangle, exploring its relationship to the triangle's sides, vertices, and the concept of the circumcircle. We'll also touch upon practical applications and further explorations.
Understanding the Circumcenter
Before focusing on right-angled triangles, let's establish a clear understanding of what a circumcenter is. The circumcenter is the point where the perpendicular bisectors of a triangle's three sides intersect. This point is equidistant from all three vertices of the triangle. The circle passing through all three vertices, centered at the circumcenter, is called the circumcircle.
The Circumcircle and its Radius
The distance from the circumcenter to each vertex is the circumradius, often denoted as R. The circumcircle's radius is crucial in various geometric calculations and theorems. For example, the area of a triangle can be expressed in terms of its sides and the circumradius using the formula: Area = (abc) / (4R), where a, b, and c are the lengths of the triangle's sides.
Locating the Circumcenter in a Right Triangle: The Special Case
Now, let's narrow our focus to right-angled triangles. The location of the circumcenter in a right-angled triangle is particularly straightforward and visually intuitive. The circumcenter of a right-angled triangle always lies at the midpoint of the hypotenuse.
This simple statement holds true for all right-angled triangles, regardless of their size or shape. Let's understand why this is the case.
Proof: Why the Circumcenter is at the Midpoint of the Hypotenuse
Consider a right-angled triangle ABC, with the right angle at vertex C. Let's denote the vertices as follows: A, B, and C.
-
Perpendicular Bisectors: The perpendicular bisector of the hypotenuse AB is a line segment that passes through the midpoint of AB and is perpendicular to AB.
-
Midpoint as the Circumcenter: This perpendicular bisector also serves as the perpendicular bisector of the side AC (since it passes through the midpoint of AB and is perpendicular to it and the midpoint is equidistant from A and B). The same logic holds true for the perpendicular bisector of BC.
-
Intersection at the Midpoint: Therefore, the intersection point of the perpendicular bisectors of AC and BC must lie on the perpendicular bisector of AB. Since the perpendicular bisector of the hypotenuse passes through the midpoint, the circumcenter coincides with the midpoint of the hypotenuse.
This simple proof demonstrates the unique characteristic of the circumcenter's location in a right-angled triangle.
Visualizing the Circumcenter
Imagine a right-angled triangle drawn on a piece of paper. Find the midpoint of the hypotenuse by folding the paper in half, aligning the two endpoints of the hypotenuse. This midpoint is precisely where the circumcenter lies. Draw a circle with the midpoint as its center and passing through the three vertices of the triangle. This is the circumcircle.
Applications and Further Explorations
Understanding the circumcenter's location in a right-angled triangle has numerous applications in various fields:
-
Geometry Problems: Many geometry problems involving right-angled triangles can be elegantly solved by utilizing the properties of the circumcenter and circumradius. For instance, determining the circumradius can be vital in calculating areas and other geometric quantities.
-
Trigonometry: The circumcenter's location plays a role in trigonometric identities and formulas related to right-angled triangles. The circumradius often appears in trigonometric calculations involving the sides and angles of right-angled triangles.
-
Coordinate Geometry: In coordinate geometry, knowing the location of the circumcenter allows you to easily determine the equation of the circumcircle. This is particularly useful when dealing with problems involving distances and positions of points.
-
Computer Graphics and CAD: In computer graphics and CAD applications, the circumcenter is a crucial point for creating circles and arcs that pass through specific points, which is often a requirement in various design tasks.
Beyond Right-Angled Triangles
While this article has focused on the circumcenter of right-angled triangles, it's important to note that the circumcenter exists for all types of triangles. However, the location of the circumcenter varies depending on the type of triangle.
-
Acute Triangles: In acute triangles (all angles less than 90 degrees), the circumcenter lies inside the triangle.
-
Obtuse Triangles: In obtuse triangles (one angle greater than 90 degrees), the circumcenter lies outside the triangle.
Understanding the differences in circumcenter location across various triangle types highlights the unique properties of right-angled triangles.
Practical Exercises
To solidify your understanding of the circumcenter's location in right-angled triangles, try these exercises:
-
Sketching: Draw several right-angled triangles of varying sizes and shapes. Locate the circumcenter by finding the midpoint of the hypotenuse in each case.
-
Coordinate Geometry: Given the coordinates of the vertices of a right-angled triangle, calculate the coordinates of the circumcenter using the midpoint formula.
-
Problem Solving: Work through geometry problems that involve calculating the circumradius or using the circumcenter's properties to solve for unknown lengths or angles.
Conclusion
The circumcenter of a right-angled triangle holds a unique and easily identifiable position: the midpoint of the hypotenuse. This simple yet powerful characteristic simplifies various geometric calculations and has broad applications across mathematics, computer graphics, and related fields. Mastering this concept is a stepping stone towards a deeper understanding of geometry and trigonometry. Through practice and exploration, you can further develop your proficiency in working with circumcenters and other geometric concepts. Remember, understanding the fundamentals is key to tackling more complex problems. Therefore, continue exploring, experimenting, and solving problems to build a robust foundation in geometry.
Latest Posts
Latest Posts
-
Which Organelle Is Responsible For Photosynthesis
Apr 01, 2025
-
Which Is Larger Pound Or Kilogram
Apr 01, 2025
-
Are Histograms And Bar Graphs The Same
Apr 01, 2025
-
How Many Vowels Are There In English Language
Apr 01, 2025
-
Two Angles That Add Up To 90 Degrees
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Where Is The Circumcenter Of A Right Triangle Located . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
