What's The Square Root Of 8
Juapaving
Mar 31, 2025 · 5 min read
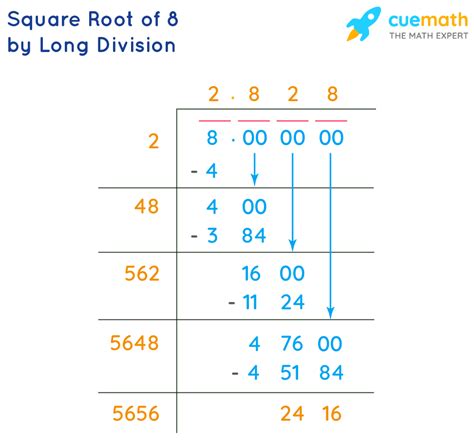
Table of Contents
- What's The Square Root Of 8
- Table of Contents
- What's the Square Root of 8? A Deep Dive into Simplification and Approximation
- Understanding Square Roots
- Simplifying the Square Root of 8
- Prime Factorization: The Key to Simplification
- Approximating the Square Root of 8
- Using a Calculator
- The Babylonian Method (or Heron's Method)
- Using Linear Approximation
- The Importance of Understanding √8
- Beyond the Basics: Exploring Related Concepts
- Conclusion: Mastering the Square Root of 8 and Beyond
- Latest Posts
- Latest Posts
- Related Post
What's the Square Root of 8? A Deep Dive into Simplification and Approximation
The seemingly simple question, "What's the square root of 8?" opens a door to a fascinating exploration of mathematical concepts, from fundamental simplification techniques to the intricacies of approximation methods. This article will delve into various ways of understanding and calculating the square root of 8, catering to both beginners and those seeking a deeper understanding.
Understanding Square Roots
Before we tackle the square root of 8 specifically, let's establish a foundational understanding of what a square root represents. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. It's the inverse operation of squaring a number.
Simplifying the Square Root of 8
The square root of 8 (√8) isn't a whole number; it's an irrational number, meaning it cannot be expressed as a simple fraction. However, we can simplify it to a more manageable form using the properties of square roots. This process involves identifying perfect square factors within the number 8.
Prime Factorization: The Key to Simplification
The most effective way to simplify a square root is through prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Let's prime factorize 8:
8 = 2 x 2 x 2 = 2³
Now, we can rewrite √8 using this factorization:
√8 = √(2 x 2 x 2)
Since √(a x a) = a, we can simplify:
√8 = √(2 x 2) x √2 = 2√2
Therefore, the simplified form of √8 is 2√2. This is the most precise and commonly accepted way to represent the square root of 8.
Approximating the Square Root of 8
While 2√2 is the exact simplified form, it's often helpful to have an approximate decimal value for practical applications. There are several ways to approximate √8:
Using a Calculator
The simplest method is to use a calculator. Most calculators have a square root function (√). Entering √8 will give you an approximate decimal value of 2.82842712475.
The Babylonian Method (or Heron's Method)
This iterative method provides a progressively more accurate approximation of a square root. It's based on an initial guess and refining it through successive calculations.
Let's start with an initial guess of 3 (since 3² = 9, which is close to 8).
Iteration 1:
- Average of the guess (3) and 8 divided by the guess: (3 + 8/3) / 2 ≈ 2.8333
Iteration 2:
- Average of the previous result (2.8333) and 8 divided by the previous result: (2.8333 + 8/2.8333) / 2 ≈ 2.8284
Notice how the approximation improves with each iteration. Continuing this process will yield increasingly accurate results, converging towards the true value of √8.
Using Linear Approximation
This method utilizes the tangent line of the square root function at a nearby point to estimate the value. Let's use the point (9, 3) since √9 = 3.
The derivative of √x is 1/(2√x). At x=9, the derivative is 1/(2√9) = 1/6.
The equation of the tangent line at (9, 3) is:
y - 3 = (1/6)(x - 9)
Substituting x = 8:
y - 3 = (1/6)(8 - 9) = -1/6
y = 3 - 1/6 ≈ 2.8333
This method provides a reasonably good approximation, though less precise than the Babylonian method for the same number of iterations.
The Importance of Understanding √8
Understanding the square root of 8 isn't just about finding a numerical answer; it's about grasping fundamental mathematical principles and developing problem-solving skills. These skills are crucial in various fields, including:
- Engineering: Calculating distances, areas, and volumes often involves working with square roots.
- Physics: Many physics formulas utilize square roots, especially those involving motion, energy, and forces.
- Computer Science: Algorithms for approximating square roots are essential for computer graphics, simulations, and game development.
- Finance: Calculating investment returns and compound interest may involve working with square roots.
Beyond the Basics: Exploring Related Concepts
The concept of the square root of 8 extends to a broader understanding of:
- Irrational Numbers: √8 highlights the existence of irrational numbers—numbers that cannot be expressed as a simple fraction. This opens the door to exploring other irrational numbers like π (pi) and e (Euler's number).
- Number Systems: Understanding different number systems, such as real numbers, rational numbers, and irrational numbers, provides a more comprehensive view of mathematics.
- Approximation Techniques: The different methods for approximating √8 showcase the power and versatility of numerical methods in solving complex problems.
Conclusion: Mastering the Square Root of 8 and Beyond
The seemingly straightforward question of "What's the square root of 8?" leads to a rich exploration of mathematical concepts and techniques. From simplifying the expression to approximating its value using different methods, we've delved into the core principles behind square roots and their applications in various fields. Mastering these concepts isn't just about knowing the answer; it's about developing a deeper understanding of mathematics and its practical relevance. By understanding the process, not just the result, you build a strong foundation for tackling more complex mathematical challenges. The ability to simplify, approximate, and understand the underlying principles associated with √8 is a testament to a strong mathematical foundation. Remember, the journey of mathematical understanding is ongoing, and every problem solved opens doors to new explorations.
Latest Posts
Latest Posts
-
Drawing Of Law Of Conservation Of Mass
Apr 03, 2025
-
A Homogeneous Mixture Is Also Called A
Apr 03, 2025
-
A Substance Formed During A Chemical Reaction
Apr 03, 2025
-
Give The Major Product Of The Following Reaction
Apr 03, 2025
-
An Npn Transistor Is Made Up Of
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
