What's The Square Root Of 40
Juapaving
Mar 29, 2025 · 4 min read
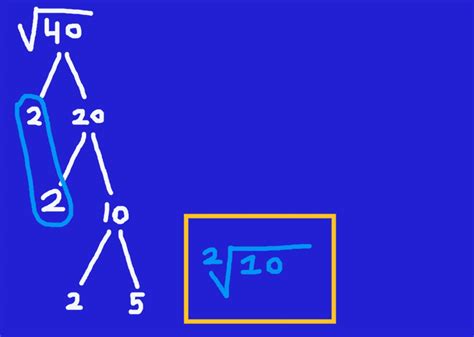
Table of Contents
- What's The Square Root Of 40
- Table of Contents
- What's the Square Root of 40? A Deep Dive into Square Roots and Approximation Techniques
- Understanding Square Roots
- Perfect Squares vs. Imperfect Squares
- Calculating the Square Root of 40
- 1. Estimation through Perfect Squares
- 2. Using a Calculator
- 3. The Babylonian Method (or Heron's Method)
- 4. The Long Division Method
- The Significance of Irrational Numbers
- Applications of Square Roots
- Beyond √40: Exploring Further
- Conclusion: More Than Just a Number
- Latest Posts
- Latest Posts
- Related Post
What's the Square Root of 40? A Deep Dive into Square Roots and Approximation Techniques
The question, "What's the square root of 40?" seems simple enough. However, exploring this seemingly straightforward query opens a door to a fascinating world of mathematical concepts, approximation techniques, and the beauty of irrational numbers. Let's embark on this journey together, uncovering not just the answer, but the underlying principles that govern square roots.
Understanding Square Roots
Before we delve into the specifics of √40, let's establish a firm understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. This concept is fundamental to algebra, geometry, and numerous other mathematical fields.
Perfect Squares vs. Imperfect Squares
Numbers like 9, 16, 25, and 36 are known as perfect squares because their square roots are whole numbers. However, 40 is not a perfect square. Its square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. This is where things get interesting.
Calculating the Square Root of 40
There isn't a single, easily calculated answer for √40 like there is for perfect squares. We'll explore several methods for finding an approximate value:
1. Estimation through Perfect Squares
The most straightforward approach is to use our knowledge of perfect squares. We know that 6 x 6 = 36 and 7 x 7 = 49. Since 40 falls between 36 and 49, we can deduce that √40 lies between 6 and 7. This gives us a rough estimate, but it's not precise enough for many applications.
2. Using a Calculator
The simplest way to find a reasonably accurate approximation is to use a calculator. Most calculators have a square root function (√). Entering √40 will yield a result close to 6.32455532. This provides a much more accurate approximation than our initial estimate. However, understanding the underlying methods behind calculator calculations is crucial for deeper comprehension.
3. The Babylonian Method (or Heron's Method)
This iterative method provides a way to approximate square roots without relying on a calculator. It's based on the principle of repeatedly refining an initial guess. Here's how it works:
-
Make an initial guess: Let's start with our initial estimate of 6.
-
Refine the guess: Divide the number (40) by the initial guess (6): 40 / 6 ≈ 6.6667
-
Average: Average the result from step 2 with the initial guess: (6 + 6.6667) / 2 ≈ 6.3333
-
Repeat: Use the result from step 3 as the new guess and repeat steps 2 and 3. Each iteration gets closer to the actual square root.
By repeating this process several times, we can achieve a remarkably accurate approximation of √40. This method demonstrates a powerful numerical technique used in various computational contexts.
4. The Long Division Method
While less commonly used today, the long division method for square roots provides a deeper understanding of the underlying mathematical processes. It involves a step-by-step algorithm that systematically refines the approximation. This method is quite involved and best explained with a detailed numerical example, exceeding the scope of this concise article.
The Significance of Irrational Numbers
The fact that √40 is an irrational number highlights a crucial aspect of mathematics. Many seemingly simple calculations lead to numbers with infinite, non-repeating decimal expansions. These numbers are essential components of various mathematical structures and have practical implications in fields like physics and engineering.
Applications of Square Roots
Square roots are not just abstract mathematical concepts; they have numerous practical applications across various disciplines:
-
Geometry: Calculating the diagonal of a square or rectangle. The Pythagorean theorem (a² + b² = c²) heavily relies on square roots.
-
Physics: Determining velocity, acceleration, or distance in kinematic equations.
-
Engineering: Design calculations involving dimensions, stress, and strain.
-
Finance: Calculating compound interest and investment returns.
-
Computer Graphics: Creating transformations and rotations in 2D and 3D spaces.
Beyond √40: Exploring Further
Understanding √40 is a stepping stone to exploring more complex mathematical concepts:
-
Higher-order roots: Cube roots (∛), fourth roots (∜), and beyond.
-
Complex numbers: Expanding the number system to include imaginary numbers, where the square root of a negative number is defined.
-
Numerical analysis: Advanced techniques for approximating solutions to complex mathematical problems.
Conclusion: More Than Just a Number
The seemingly simple question, "What's the square root of 40?" leads to a rich exploration of mathematical principles, approximation techniques, and the significance of irrational numbers. Understanding square roots is fundamental to various scientific and engineering disciplines, highlighting the practical relevance of this fundamental mathematical operation. While a calculator provides a quick answer, understanding the underlying methods provides a deeper appreciation of the beauty and power of mathematics. From estimation to iterative methods, several approaches allow us to accurately approximate √40, showcasing the diverse tools available for solving mathematical problems. The journey to understanding √40 is not just about finding a numerical value; it's about understanding the underlying concepts and their broader significance.
Latest Posts
Latest Posts
-
Ability To Run Multiple Applications Simultaneously
Apr 02, 2025
-
What Are The Vertical Rows On The Periodic Table Called
Apr 02, 2025
-
What Do You Call The Place Where An Organism Lives
Apr 02, 2025
-
What Are The Common Multiples Of 6 And 9
Apr 02, 2025
-
Are Angiosperms Gametophyte Or Sporophyte Dominant
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
