Whats The Square Root Of 121
Juapaving
Mar 21, 2025 · 5 min read
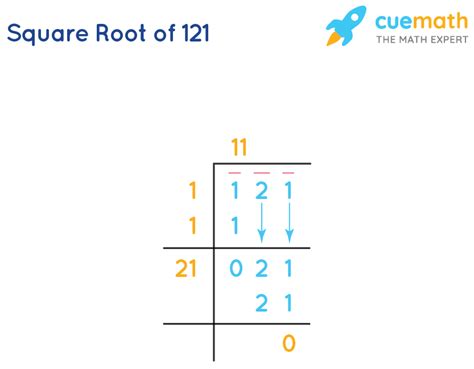
Table of Contents
What's the Square Root of 121? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What's the square root of 121?" opens a door to a fascinating world of mathematics. While the answer itself is straightforward (11), exploring the concept of square roots reveals its significance in various fields, from basic arithmetic to advanced engineering. This article will not only answer the question directly but also delve into the underlying principles, explore different methods for finding square roots, and showcase their practical applications.
Understanding Square Roots: The Fundamentals
Before jumping into the specific case of the square root of 121, let's establish a solid foundation. A square root of a number is a value that, when multiplied by itself, gives the original number. In simpler terms, it's the inverse operation of squaring a number. If we square a number 'x' (multiply it by itself, resulting in x²), then taking the square root of x² will return the original number 'x'.
For example:
- 5² = 25, so the square root of 25 is 5.
- 8² = 64, so the square root of 64 is 8.
This relationship forms the basis for understanding square roots and their applications. It's important to note that most numbers have two square roots: a positive and a negative one. For example, the square root of 25 is both +5 and -5 because (+5) * (+5) = 25 and (-5) * (-5) = 25. However, when we talk about "the" square root, we usually mean the principal square root, which is the positive square root.
Calculating the Square Root of 121
Now, let's tackle the question at hand: what's the square root of 121?
The most straightforward way to find the square root of 121 is to consider the perfect squares. Perfect squares are numbers obtained by squaring whole numbers. We can list them:
1² = 1 2² = 4 3² = 9 4² = 16 5² = 25 6² = 36 7² = 49 8² = 64 9² = 81 10² = 100 11² = 121 12² = 144
By examining this list, we see that 11² = 121. Therefore, the square root of 121 is 11. This is the principal square root; the other square root is -11.
Methods for Finding Square Roots
While simple perfect squares are easily identifiable, finding the square root of more complex numbers requires different approaches:
1. Prime Factorization Method:
This method is particularly useful for numbers that can be easily factored into prime numbers. Prime factorization involves breaking a number down into its prime factors (numbers divisible only by 1 and themselves).
Let's consider a different example: finding the square root of 36.
- Factorize: 36 = 2 x 2 x 3 x 3 = 2² x 3²
- Pair up: Notice that we have pairs of 2 and 3.
- Calculate: The square root is obtained by taking one factor from each pair: √36 = 2 x 3 = 6
This method is effective for numbers with readily identifiable prime factors.
2. Long Division Method:
The long division method is a more general approach for finding square roots, particularly for larger numbers. It's a step-by-step process that involves grouping digits and performing iterative calculations. This method is too complex to fully demonstrate here but is easily searchable online.
3. Using a Calculator:
Modern calculators have built-in functions to calculate square roots quickly and efficiently. This is often the most practical approach for everyday calculations. Simply input the number (121 in this case) and press the square root button (√).
4. Estimation and Approximation:
For numbers that aren't perfect squares, estimation can be helpful. By comparing the number to nearby perfect squares, you can get a reasonable approximation.
For instance, if we want to estimate the square root of 125, we know it's between 11 (√121) and 12 (√144). A closer approximation can be found using more sophisticated estimation techniques.
Applications of Square Roots in Real Life
Square roots have wide-ranging applications across numerous fields:
1. Geometry and Trigonometry:
- Calculating distances: The Pythagorean theorem (a² + b² = c²) utilizes square roots to find the length of the hypotenuse (c) of a right-angled triangle, given the lengths of the other two sides (a and b). This is crucial in surveying, construction, and navigation.
- Calculating areas and volumes: Finding the area of a square or the volume of a cube involves square roots. For example, if you know the area of a square, the square root of the area will give you the side length.
- Trigonometry: Many trigonometric functions and formulas involve square roots.
2. Physics and Engineering:
- Calculating velocity and acceleration: Many physics formulas involve square roots, for example, when calculating the velocity of an object under gravity or the acceleration of a moving object.
- Signal processing: Square roots are used in signal processing and data analysis, for example, when calculating the root mean square (RMS) of a signal.
- Engineering design: Square roots appear frequently in structural engineering calculations, for instance, when calculating the stress on a beam or column.
3. Finance and Economics:
- Standard deviation: In finance, the standard deviation of a stock or portfolio uses square roots to quantify risk.
- Compound interest calculations: While not directly using square roots, compound interest calculations are inherently related to exponential growth, which is linked to square roots through logarithmic transformations.
4. Computer Graphics and Gaming:
- 3D rendering: Square roots are essential in rendering 3D graphics, often used in vector calculations and transformations.
- Game physics: Game physics engines rely heavily on square roots for distance calculations and vector operations.
5. Statistics and Data Analysis:
- Standard error: The standard error of the mean, used to estimate the uncertainty of sample means, uses square roots.
- Correlation coefficients: Some statistical analyses involve square roots when calculating correlation coefficients that describe the relationship between variables.
Conclusion: Beyond the Simple Answer
While the answer to "What's the square root of 121?" is simply 11, exploring the concept delves into a fundamental mathematical operation with vast practical applications. Understanding square roots isn't just about memorizing a formula; it's about grasping a concept that underpins many aspects of science, engineering, finance, and technology. From the simple act of measuring the side of a square to complex calculations in physics and engineering, the square root function remains a powerful tool in our mathematical arsenal. This comprehensive exploration has hopefully shed light on the importance and versatility of this seemingly simple mathematical concept.
Latest Posts
Latest Posts
-
What Is The S I Unit For Temperature
Mar 27, 2025
-
Write A Short Note On Apiculture
Mar 27, 2025
-
Dissolving Sugar In Water Is A Chemical Change
Mar 27, 2025
-
Which Of The Following Is An Abstract Word
Mar 27, 2025
-
What Type Of Wave Is Water Wave
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of 121 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
