What's The Square Root Of 100
Juapaving
Apr 02, 2025 · 6 min read
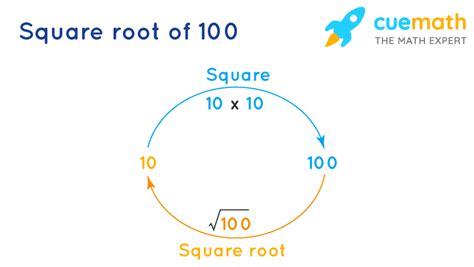
Table of Contents
What's the Square Root of 100? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What's the square root of 100?" opens a door to a fascinating world of mathematics, encompassing fundamental concepts, practical applications, and even surprising connections to other fields. While the answer itself is straightforward (10), the journey to understanding it, and the broader implications of square roots, is far more enriching. This article will explore the square root of 100, delve into the concept of square roots, and examine their significance in various disciplines.
Understanding Square Roots: The Basics
Before we definitively answer what the square root of 100 is, let's establish a firm understanding of the fundamental concept. A square root of a number is a value that, when multiplied by itself (squared), gives the original number. In simpler terms, it's the inverse operation of squaring a number.
For instance:
- 2 x 2 = 4, therefore, the square root of 4 is 2 (√4 = 2).
- 3 x 3 = 9, therefore, the square root of 9 is 3 (√9 = 3).
- 10 x 10 = 100, therefore, the square root of 100 is 10 (√100 = 10).
This is the core principle that governs all square root calculations. It's important to note that most numbers have two square roots: a positive and a negative. However, when we talk about the square root, we usually refer to the principal square root, which is the positive value. In the case of 100, while both 10 and -10 squared equal 100, the principal square root is 10.
Calculating the Square Root of 100: Different Methods
While the square root of 100 is readily apparent for smaller, perfect squares, let's explore some methods to calculate square roots, applicable to both perfect and imperfect squares:
1. Prime Factorization Method (For Perfect Squares)
This method is particularly useful for perfect squares, which are numbers that result from squaring an integer. The process involves:
- Prime Factorization: Break down the number into its prime factors. For 100, this is 2 x 2 x 5 x 5 (or 2² x 5²).
- Pairing Factors: Look for pairs of identical prime factors. We have a pair of 2s and a pair of 5s.
- Calculate the Square Root: Take one factor from each pair and multiply them together. In this case, 2 x 5 = 10. Therefore, the square root of 100 is 10.
This method provides a clear visual representation of the square root concept, highlighting the pairing of factors that results in the original number when squared.
2. Using a Calculator
The simplest method for finding the square root of any number, including 100, is to use a calculator. Most calculators have a dedicated square root function (√) that directly provides the answer. Simply input 100 and press the square root button; the result will be 10. This method is efficient and accurate, especially for larger or imperfect squares.
3. Long Division Method (For Approximations)
For imperfect squares, or for educational purposes in understanding the mechanics of square root calculation, the long division method can be used. While more complex, it's a valuable technique for understanding the iterative process of approximating square roots. This method is less efficient than a calculator for simple numbers like 100 but serves as a strong foundation for understanding the process in more complex cases. Detailed explanations of this method can be found in various mathematical resources.
Applications of Square Roots: Beyond the Basics
The seemingly simple concept of square roots extends far beyond basic arithmetic. They are integral to numerous fields, including:
1. Geometry and Trigonometry
Square roots are fundamental in geometry. Calculating the length of the hypotenuse of a right-angled triangle uses the Pythagorean theorem (a² + b² = c²), which inherently involves square roots. Determining distances, areas, and volumes of various geometric shapes frequently requires the calculation of square roots. Trigonometry, closely related to geometry, also utilizes square roots extensively in its formulas and calculations.
2. Physics and Engineering
Many physical phenomena and engineering calculations rely on square roots. For instance, calculating the velocity of an object requires manipulating equations involving square roots. In electrical engineering, understanding impedance and reactance involves square roots. The study of motion, energy, and forces relies heavily on square root calculations.
3. Statistics and Data Analysis
Square roots play a crucial role in statistical analysis, appearing in various formulas and calculations, including standard deviation and variance. These calculations help assess the spread and distribution of data sets, making them crucial in various fields from finance to social sciences. Standard deviation, a measure of how spread out numbers are, fundamentally uses square roots in its calculation.
4. Computer Graphics and Game Development
Square roots are essential in computer graphics and game development for tasks such as calculating distances between points, determining the magnitude of vectors, and performing various geometric transformations. These calculations are vital for creating realistic and accurate representations of objects and environments. The rendering of images, for example, frequently uses calculations involving square roots.
5. Financial Modeling and Investments
In finance, square roots are used in various financial models and investment strategies. Calculating the volatility of an asset, assessing portfolio risk, and pricing options all frequently involve square root calculations. Understanding the standard deviation of investment returns, a key factor in investment decision-making, requires applying square roots.
6. Computer Science and Algorithm Design
Square roots appear in various algorithms and data structures used in computer science. Algorithms involving searches, sorting, and graph traversal often utilize square root computations to optimize performance and efficiency. The complexity analysis of algorithms frequently incorporates square roots to estimate resource consumption.
Beyond the Square Root of 100: Expanding Our Understanding
While the square root of 100 is a straightforward calculation, understanding the broader concept of square roots, the methods of their calculation, and their extensive applications across diverse fields is crucial. The exploration of this seemingly simple concept opens up a world of mathematical possibilities and practical applications.
This journey of understanding the square root of 100 expands to include exploring more complex square roots, including those of non-perfect squares (where the answer isn't a whole number) and utilizing advanced computational methods for accurate approximations. The study of square roots isn't just about finding a single numerical answer but involves delving into mathematical processes and understanding the fundamental principles behind them.
From the basics of arithmetic to the complexities of advanced algorithms, the square root of 100 serves as a launching point for a richer appreciation of mathematics and its integral role in the world around us. Its seemingly simple calculation unlocks a deeper understanding of a fundamental concept with wide-ranging and crucial applications.
Latest Posts
Latest Posts
-
Can The Quotient Of Two Irrational Numbers Be Rational
Apr 03, 2025
-
12 Cm Is What In Inches
Apr 03, 2025
-
How Many Liters In 100 Gallons
Apr 03, 2025
-
Are Minerals A Renewable Resource Why Or Why Not
Apr 03, 2025
-
What Organelles Are Found Only In Plant Cells
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
