Can The Quotient Of Two Irrational Numbers Be Rational
Juapaving
Apr 03, 2025 · 5 min read
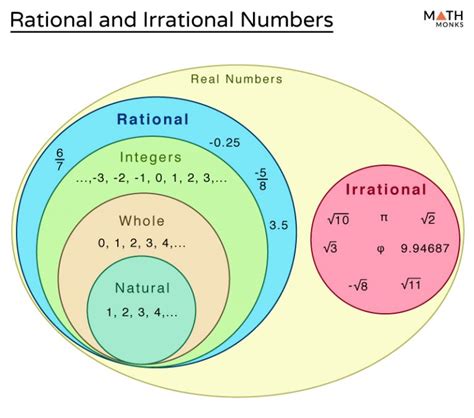
Table of Contents
Can the Quotient of Two Irrational Numbers Be Rational?
The question of whether the quotient of two irrational numbers can be rational is a fascinating exploration into the intricacies of number theory. At first glance, it might seem improbable. After all, irrational numbers are defined by their inability to be expressed as a simple fraction of two integers. However, a deeper dive reveals a surprising and elegant answer. Let's unravel this mathematical mystery, examining the underlying principles and providing concrete examples.
Understanding Irrational and Rational Numbers
Before we delve into the quotient, let's solidify our understanding of the key players: rational and irrational numbers.
Rational Numbers: The Fraction Family
Rational numbers are numbers that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. This seemingly simple definition encompasses a vast range of numbers, including:
- Integers: Whole numbers, both positive and negative (e.g., -3, 0, 5).
- Fractions: Numbers expressed as ratios of integers (e.g., 1/2, -3/4, 7/1).
- Terminating Decimals: Decimals that end after a finite number of digits (e.g., 0.75, 2.5, -3.125). These can always be converted into fractions.
- Repeating Decimals: Decimals with a pattern of digits that repeats infinitely (e.g., 0.333..., 1.232323..., -0.142857142857...). These too can be expressed as fractions.
Irrational Numbers: Beyond Fractions
Irrational numbers, on the other hand, cannot be expressed as a fraction of two integers. Their decimal representation is non-terminating and non-repeating, meaning they go on forever without exhibiting any repeating pattern. Famous examples include:
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159...
- e (Euler's number): The base of the natural logarithm, approximately 2.71828...
- √2 (Square root of 2): The number that, when multiplied by itself, equals 2. Its decimal representation is approximately 1.41421...
Exploring the Quotient: Can Irrational/Irrational = Rational?
Now, let's address the central question: can the division of two irrational numbers result in a rational number? The answer is a resounding yes. This might seem counterintuitive, but we can demonstrate it with examples.
Example 1: The Power of √2
Let's consider the irrational number √2. If we divide √2 by itself, we get:
√2 / √2 = 1
Here, the quotient of two irrational numbers (√2 and √2) is the rational number 1. This simple example clearly shows the possibility.
Example 2: A More Complex Illustration
Let's use a slightly more intricate example. Consider the following two irrational numbers:
- a = √2
- b = 2√2
Now, let's calculate their quotient:
a / b = √2 / (2√2) = 1/2
Again, the quotient of two irrational numbers (√2 and 2√2) is a rational number, specifically 1/2.
Generalizing the Phenomenon
These examples illustrate a broader principle. We can create countless pairs of irrational numbers whose quotient is rational. The key is to strategically construct the irrational numbers such that their specific properties cancel out upon division, leaving behind a simple fraction.
Constructing Irrational Numbers with Rational Quotients
The ability to find irrational numbers with rational quotients highlights a crucial aspect of irrational numbers: they are not a monolithic, uniform set. Their properties can vary significantly, leading to interesting interactions when performing mathematical operations like division.
We can generalize the method of constructing such pairs. Consider two irrational numbers, 'x' and 'y', where 'y' is a rational multiple of 'x'. Then, 'y' can be expressed as 'rx', where 'r' is a rational number. The quotient would be:
x / y = x / (rx) = 1/r
Since 'r' is rational, 1/r will also be rational (unless r = 0). This demonstrates a systematic way of generating pairs of irrational numbers with rational quotients.
The Significance of This Mathematical Result
The fact that the quotient of two irrational numbers can be rational has implications beyond simple mathematical curiosity. It demonstrates the rich and nuanced nature of irrational numbers and highlights the interconnectedness of different number systems within mathematics. It reminds us that seemingly disparate mathematical entities can interact in unexpected and elegant ways.
This concept is crucial for a deeper understanding of:
- Number Theory: This result adds to our comprehension of the structure and properties of different number sets.
- Real Analysis: It plays a role in the study of limits, continuity, and other fundamental concepts.
- Algebra: The construction of irrational numbers with rational quotients is a valuable exercise in algebraic manipulation.
Beyond Simple Examples: Exploring Deeper Implications
While the simple examples provided offer clear demonstrations, the true depth of this concept lies in its potential for more complex explorations. Consider the following:
- Infinitely many pairs: There are infinitely many pairs of irrational numbers whose quotient is rational. This further underscores the rich tapestry of mathematical relationships.
- Transcendental numbers: The concept extends beyond simple algebraic irrationals. We can also find pairs of transcendental numbers (numbers that are not roots of any polynomial equation with rational coefficients) whose quotient is rational. This expands the applicability and significance of the concept significantly.
The study of the quotient of irrational numbers is not just about finding specific examples; it’s about understanding the underlying mathematical structure and relationships that govern these numbers. It’s about recognizing the unexpected beauty and elegance that often emerge from seemingly simple questions in mathematics.
Conclusion: A Glimpse into Mathematical Depth
The seemingly simple question of whether the quotient of two irrational numbers can be rational leads us to a profound exploration of the nature of numbers and their interactions. The answer, a definitive yes, is not just a mathematical fact; it is a gateway to deeper understanding of the rich and interconnected world of numbers, highlighting the elegance and unexpected beauty within mathematics itself. The examples provided, along with the principles explained, illustrate how seemingly disparate mathematical concepts can converge to reveal a harmonious and fascinating interplay. The journey of understanding this phenomenon is as enriching as the destination itself, prompting further exploration into the intricacies of number theory and its diverse applications.
Latest Posts
Latest Posts
-
Where In A Eukaryotic Cell Does Transcription Occur
Apr 04, 2025
-
Distance Covered Per Unit Of Time Is Called
Apr 04, 2025
-
What Is A Herd Of Kangaroos Called
Apr 04, 2025
-
How To Write A Check For 11550
Apr 04, 2025
-
Cbse Class 6th Maths Book Pdf
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Can The Quotient Of Two Irrational Numbers Be Rational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
