What's The Square Root Of 10
Juapaving
Mar 25, 2025 · 4 min read
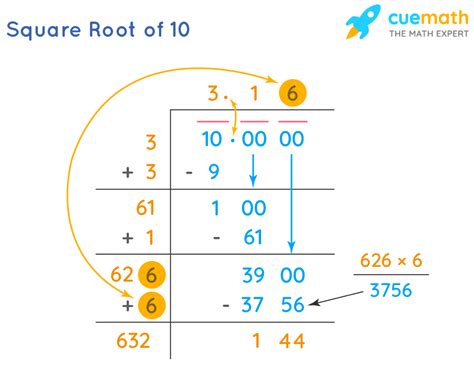
Table of Contents
What's the Square Root of 10? Exploring the Number and its Applications
The square root of 10, denoted as √10, is a fascinating number that blends simplicity in its concept with complexity in its precise representation. While it's easy to understand what it means – the number that, when multiplied by itself, equals 10 – actually pinning down its value requires a deeper dive into mathematics. This article explores √10 from multiple perspectives, investigating its approximate value, its significance in various mathematical contexts, and its applications in real-world scenarios.
Understanding Square Roots
Before delving into the specifics of √10, let's refresh our understanding of square roots. A square root of a number x is a number y such that y² = x. In simpler terms, it's the number that, when multiplied by itself, gives you the original number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
Importantly, most numbers don't have a "neat" whole number or simple fraction as their square root. These are called irrational numbers, and √10 falls squarely (pun intended!) into this category. This means its decimal representation goes on forever without repeating.
Approximating the Square Root of 10
Since √10 is irrational, we can only approximate its value. Several methods exist to do this:
1. Using a Calculator
The simplest method is to use a calculator. Most calculators will provide a value of approximately 3.16227766. This is accurate to several decimal places, sufficient for most practical applications.
2. The Babylonian Method (or Heron's Method)
This iterative method provides increasingly accurate approximations. Start with an initial guess (let's say 3), and then repeatedly apply the following formula:
x_(n+1) = 0.5 * (x_n + 10/x_n)
Where:
x_nis the current guessx_(n+1)is the next, improved guess
Let's illustrate:
- Iteration 1:
x_1 = 0.5 * (3 + 10/3) ≈ 3.1667 - Iteration 2:
x_2 = 0.5 * (3.1667 + 10/3.1667) ≈ 3.16228 - Iteration 3:
x_3 = 0.5 * (3.16228 + 10/3.16228) ≈ 3.16227766
As you can see, the approximation rapidly converges to the actual value.
3. Linear Interpolation
This method uses the knowledge that √9 = 3 and √16 = 4. Since 10 lies between 9 and 16, we can approximate √10 by linearly interpolating:
√10 ≈ 3 + (10 - 9) * (4 - 3) / (16 - 9) ≈ 3.14
This method provides a less precise approximation, but it illustrates the concept of estimating square roots based on known values.
√10 in Mathematical Contexts
The square root of 10 appears in various mathematical settings:
1. Geometry
√10 represents the length of the hypotenuse of a right-angled triangle with legs of length 1 and 3 (using the Pythagorean theorem: a² + b² = c²). This geometric interpretation provides a visual understanding of the number.
2. Number Theory
As an irrational number, √10 plays a role in exploring the properties of irrational numbers and their relationships with rational numbers. It's a member of a larger set of numbers with similar characteristics.
3. Algebra
√10 frequently appears in algebraic equations and expressions. Solving equations may involve simplifying expressions containing √10 or manipulating them to find solutions.
4. Calculus
In calculus, √10 might be encountered when evaluating integrals or derivatives involving square roots. Its irrational nature requires careful handling of limits and approximations.
Real-World Applications
While it might seem abstract, √10 finds practical uses in various fields:
1. Engineering and Physics
In engineering and physics, calculations involving distances, forces, or velocities often lead to expressions with square roots. For instance, calculating the diagonal of a rectangular object with dimensions 1 and 3 units would involve √10.
2. Construction and Architecture
Determining diagonal measurements, calculating material quantities for sloped roofs, or designing structures with specific angles all rely on understanding and calculating square roots, including √10.
3. Computer Graphics and Game Development
Generating realistic 2D and 3D graphics often requires manipulating vectors and coordinates. Calculations involving distances and angles will often involve square roots.
4. Statistics and Data Analysis
In statistics, the standard deviation, a crucial measure of data dispersion, involves square roots. Data sets producing a variance of 10 would have a standard deviation of √10.
Conclusion: The Enduring Significance of √10
The square root of 10, despite its seemingly simple definition, reveals itself to be a rich and multifaceted number. Its irrationality underscores the vastness of the number system, while its presence in various mathematical and real-world applications showcases its practical significance. From geometric interpretations to its use in advanced calculations, √10 serves as a reminder of the interconnectedness and beauty found within mathematics. Understanding its approximation and its appearance in different contexts allows for a deeper appreciation of its place within the broader landscape of mathematical concepts. While a calculator provides an easy solution for its numerical value, understanding the underlying principles and the methods for approximating √10 broadens our mathematical understanding and problem-solving capabilities. This exploration of √10 ultimately highlights the importance of combining theoretical knowledge with practical applications in navigating the world of mathematics.
Latest Posts
Latest Posts
-
Cuanto Es 15 Inches En Centimetros
May 09, 2025
-
The Least Common Multiple Of 12 And 8
May 09, 2025
-
Is 5 7 A Rational Number
May 09, 2025
-
How To Find Minors Of Matrix
May 09, 2025
-
This Is The Process Of Copying Dna To Rna
May 09, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.