Whats The Lcm Of 8 And 10
Juapaving
Mar 25, 2025 · 5 min read
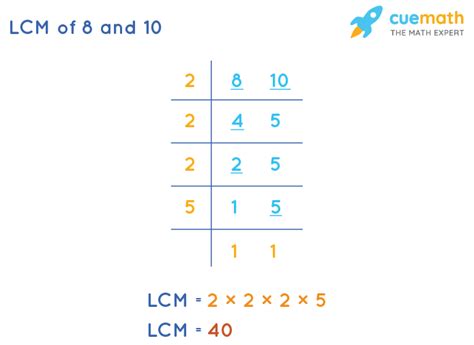
Table of Contents
What's the LCM of 8 and 10? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be incredibly valuable, especially in various mathematical and real-world applications. This article explores the LCM of 8 and 10 in detail, examining several approaches and highlighting their significance. We'll go beyond just finding the answer and delve into the theory, providing a comprehensive guide for anyone wanting to master LCM calculations.
Understanding Least Common Multiples (LCM)
Before we tackle the LCM of 8 and 10, let's clarify what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
Think of it like this: Imagine you have two gears with 8 and 10 teeth respectively. The LCM represents the smallest number of rotations needed for both gears to simultaneously return to their starting positions. This analogy helps visualize the practical application of LCMs.
Method 1: Listing Multiples
One of the simplest methods, although less efficient for larger numbers, involves listing the multiples of each number until a common multiple is found.
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
Notice that 40 and 80 appear in both lists. However, 40 is the smallest number present in both lists, making it the least common multiple of 8 and 10.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Prime factorization of 8: 2 x 2 x 2 = 2³
Prime factorization of 10: 2 x 5
To find the LCM using prime factorization:
- Identify all the prime factors: In this case, we have 2 and 5.
- Take the highest power of each prime factor: The highest power of 2 is 2³ (from the factorization of 8), and the highest power of 5 is 5¹ (from the factorization of 10).
- Multiply the highest powers together: 2³ x 5 = 8 x 5 = 40
Therefore, the LCM of 8 and 10 is 40. This method is generally preferred for its efficiency and systematic approach.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
First, let's find the GCD of 8 and 10. The divisors of 8 are 1, 2, 4, and 8. The divisors of 10 are 1, 2, 5, and 10. The greatest common divisor is 2.
Now, apply the formula:
LCM(8, 10) = (8 x 10) / 2 = 80 / 2 = 40
This confirms our previous findings. This method is particularly useful when dealing with larger numbers where prime factorization might become cumbersome. Efficient algorithms exist for finding the GCD, further streamlining this approach.
Real-World Applications of LCM
Understanding LCMs isn't just an academic exercise; it has practical applications in many fields:
- Scheduling: Imagine two buses depart from a station at different intervals. The LCM helps determine when both buses will depart simultaneously again.
- Construction: In construction projects, materials often need to be cut into specific lengths. The LCM helps determine the largest possible piece that can be cut without any waste.
- Music: In music theory, LCMs are used to determine the least common denominator for rhythmic patterns, ensuring harmonious combinations.
- Science: Periodic phenomena, such as planetary orbits or radioactive decay, frequently involve LCM calculations to predict cyclical events.
- Computer Science: In algorithms and data structures, LCMs are crucial in problems involving synchronization and cycle detection.
These examples demonstrate the broad utility of LCMs, extending beyond basic arithmetic into diverse areas.
Beyond Two Numbers: LCM of Multiple Numbers
The principles discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly well-suited for this. You would factorize each number into its prime factors, then take the highest power of each distinct prime factor present and multiply them together to obtain the LCM.
For example, let's find the LCM of 8, 10, and 12:
- Prime factorization of 8: 2³
- Prime factorization of 10: 2 x 5
- Prime factorization of 12: 2² x 3
The distinct prime factors are 2, 3, and 5. The highest power of each is 2³, 3¹, and 5¹. Therefore, the LCM(8, 10, 12) = 2³ x 3 x 5 = 8 x 3 x 5 = 120.
Conclusion: Mastering LCM Calculations
Finding the LCM of 8 and 10, as demonstrated, can be approached through multiple methods. While listing multiples is intuitive, prime factorization provides a more efficient and systematic approach, especially for larger numbers. The GCD method offers an alternative, leveraging the relationship between LCM and GCD. Understanding these methods and their underlying principles empowers you to confidently tackle LCM problems, appreciating their significance in various mathematical and practical contexts. Remember that choosing the right method depends on the specific numbers and the context of the problem. For smaller numbers, listing multiples might suffice, while for larger numbers, prime factorization or the GCD method is generally more efficient. Ultimately, mastering LCM calculations enhances your mathematical proficiency and problem-solving skills. The practical applications of LCMs demonstrate its value beyond the realm of abstract mathematics, highlighting its relevance in real-world scenarios.
Latest Posts
Latest Posts
-
Write A Short Note On Apiculture
Mar 27, 2025
-
Dissolving Sugar In Water Is A Chemical Change
Mar 27, 2025
-
Which Of The Following Is An Abstract Word
Mar 27, 2025
-
What Type Of Wave Is Water Wave
Mar 27, 2025
-
How Many Electrons Are Shared By A Triple Bond
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Whats The Lcm Of 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
