What's The Difference Between A Rhombus And A Parallelogram
Juapaving
Mar 27, 2025 · 5 min read
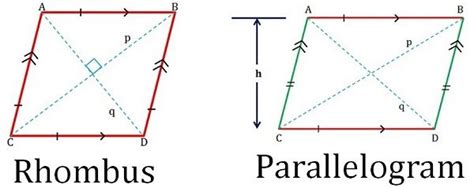
Table of Contents
What's the Difference Between a Rhombus and a Parallelogram? A Deep Dive into Quadrilaterals
Understanding the nuances between different geometric shapes can be tricky, especially when dealing with quadrilaterals – four-sided polygons. Two shapes that often cause confusion are the rhombus and the parallelogram. While closely related, they possess distinct characteristics that set them apart. This comprehensive guide will delve into the definitions, properties, and differences between these two fundamental shapes, equipping you with a solid grasp of their unique features.
Defining the Parallelogram
A parallelogram is a quadrilateral where opposite sides are parallel and equal in length. This fundamental property forms the basis for several other characteristics we'll explore. Imagine pushing or pulling on a perfectly square picture frame; as long as the opposite sides remain parallel, the frame transforms into a parallelogram. The key here is the parallelism of opposite sides.
Key Properties of a Parallelogram:
- Opposite sides are parallel: This is the defining characteristic.
- Opposite sides are congruent (equal in length): A direct consequence of parallel sides.
- Opposite angles are congruent: The angles opposite each other are always equal in measure.
- Consecutive angles are supplementary: Adjacent angles add up to 180 degrees. This means that if one angle is 60 degrees, its neighboring angle will be 120 degrees.
- Diagonals bisect each other: The diagonals intersect at their midpoints, dividing each other into two equal segments.
This last point is particularly useful for problem-solving and proving theorems related to parallelograms. Understanding these properties allows for accurate calculation of angles, side lengths, and areas.
Understanding the Rhombus
A rhombus, often called a diamond, is a special type of parallelogram. This means it possesses all the properties of a parallelogram, but it adds a crucial extra feature: all four sides are equal in length. Think of a square that's been "tilted" – it's still a parallelogram, but with the added constraint of equal side lengths, it becomes a rhombus.
Key Properties of a Rhombus:
- All sides are congruent (equal in length): This is the defining property that distinguishes a rhombus from a general parallelogram.
- Opposite sides are parallel: Inherited from its parallelogram nature.
- Opposite angles are congruent: Again, inherited from parallelogram properties.
- Consecutive angles are supplementary: Another property inherited from parallelograms.
- Diagonals bisect each other: This property is also inherited from parallelograms.
- Diagonals are perpendicular bisectors: This is a unique property of rhombuses. The diagonals intersect at a right angle (90 degrees) and bisect each other.
- Diagonals bisect the angles: Each diagonal divides its opposite angles into two equal angles.
The perpendicularity of the diagonals is a crucial difference between a rhombus and a parallelogram. This property creates four congruent right-angled triangles within the rhombus. This geometric fact is frequently used in calculations of area and other geometric properties.
The Venn Diagram of Understanding: Parallelograms and Rhombuses
To visualize the relationship, imagine a Venn diagram. The larger circle represents all parallelograms. Inside this larger circle, a smaller circle represents all rhombuses. Every rhombus is a parallelogram, but not every parallelogram is a rhombus. This illustrates the hierarchical relationship: a rhombus is a specialized type of parallelogram with an additional constraint (equal side lengths).
Exploring the Differences: A Comparative Table
To further highlight the distinctions, let's summarize the key differences in a concise table:
| Feature | Parallelogram | Rhombus |
|---|---|---|
| Side Lengths | Opposite sides are equal | All four sides are equal |
| Angles | Opposite angles are equal, consecutive angles are supplementary | Opposite angles are equal, consecutive angles are supplementary |
| Diagonals | Bisect each other | Bisect each other, are perpendicular bisectors, bisect the angles |
| Shape | Can be rectangular, square, or oblique | Always has equal sides, can be a square |
Beyond the Basics: Squares and Rectangles
The relationship extends further. A square is a special case of both a parallelogram and a rhombus. It satisfies all the properties of both shapes: equal sides, parallel sides, and right angles. Similarly, a rectangle is a special type of parallelogram with four right angles.
Practical Applications and Problem Solving
Understanding the differences between parallelograms and rhombuses has practical applications in various fields:
- Engineering and Architecture: Parallelogram and rhombus shapes are utilized in structural designs, trusses, and bracing systems to ensure stability and distribute weight effectively.
- Physics: Analyzing forces and vectors often involves understanding parallelogram properties, especially in resolving forces into components.
- Computer Graphics: These shapes are fundamental building blocks in computer-aided design (CAD) and other graphics software.
- Mathematics: These shapes provide foundational concepts for advanced geometric studies, including trigonometry and calculus.
Solving Problems Involving Parallelograms and Rhombuses
Let's tackle a few examples to solidify our understanding:
Example 1: A parallelogram has one angle measuring 70 degrees. What are the measures of the other three angles?
- Solution: Since consecutive angles are supplementary, the adjacent angle measures 180 - 70 = 110 degrees. Opposite angles are equal, so the other two angles also measure 70 and 110 degrees.
Example 2: A rhombus has diagonals of length 6 cm and 8 cm. What is its area?
- Solution: The diagonals of a rhombus are perpendicular bisectors. They divide the rhombus into four congruent right-angled triangles. The area of one triangle is (1/2) * (6/2) * (8/2) = 6 cm². Since there are four such triangles, the total area of the rhombus is 4 * 6 = 24 cm².
Example 3: Prove that the diagonals of a rhombus are perpendicular bisectors.
- Solution: This requires a more formal geometric proof utilizing congruent triangles and properties of parallelograms. The proof involves showing that the triangles formed by the diagonals are congruent using the Side-Side-Side (SSS) congruence theorem and then demonstrating that the angles where the diagonals intersect are right angles. This proof often uses the properties of isosceles triangles formed by the equal sides of the rhombus.
Conclusion
The differences between parallelograms and rhombuses, while subtle, are significant. Understanding the defining properties of each shape – parallelism of opposite sides for parallelograms and equal side lengths for rhombuses – is crucial for solving geometric problems and applying these concepts in various fields. Remember, a rhombus is a specialized type of parallelogram, inheriting all its properties while adding the crucial feature of equal side lengths. This comprehensive understanding allows for accurate analysis and application of these fundamental geometric shapes in diverse contexts. By mastering these concepts, you'll gain a deeper appreciation for the elegance and utility of geometric principles.
Latest Posts
Latest Posts
-
How To Tell Time On A Watch Without Numbers
Mar 30, 2025
-
How Many Km Are In 230 M
Mar 30, 2025
-
Definition Of Word Form In Math
Mar 30, 2025
-
How Much Is 200 Fahrenheit In Celsius
Mar 30, 2025
-
What Is A Adjacent Supplementary Angle
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What's The Difference Between A Rhombus And A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
