Whats A Shape With 8 Vertices And 6 Faces.
Juapaving
Apr 02, 2025 · 6 min read
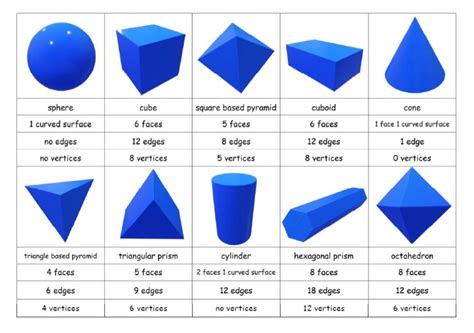
Table of Contents
What's a Shape with 8 Vertices and 6 Faces? Unraveling the Octahedron
Have you ever pondered the fascinating world of geometry? Beyond the familiar squares and circles, lies a universe of three-dimensional shapes with unique properties. One such shape, captivating in its symmetry and elegance, is defined by possessing exactly eight vertices and six faces. This article will delve deep into the characteristics, properties, and applications of this intriguing geometrical solid: the octahedron.
Understanding the Fundamentals: Vertices, Edges, and Faces
Before we explore the octahedron, let's establish a common understanding of key geometrical terms:
- Vertices: These are the points where the edges of a three-dimensional shape meet. Think of them as the corners of the shape.
- Edges: These are the line segments that connect two vertices. They form the "skeleton" of the solid.
- Faces: These are the flat surfaces that enclose the solid. They are polygons, meaning they are closed shapes with straight sides.
With these definitions in mind, we can now specifically address the shape in question: a solid with 8 vertices and 6 faces. This uniquely describes a regular octahedron. However, it's important to note that variations exist; there are irregular octahedra, where the faces and edges are not all equal in size.
Delving into the Regular Octahedron: A Closer Look
The regular octahedron holds a special place in geometry due to its high degree of symmetry. Each face is an equilateral triangle, and all the edges are of equal length. This perfect symmetry leads to a number of interesting properties:
Symmetry and its Implications
The regular octahedron exhibits a remarkable level of symmetry. It possesses several planes of symmetry, meaning you could cut it in half along certain planes and get two mirror images. This symmetry is reflected in its rotational symmetry as well, meaning you can rotate it around certain axes and it will still look the same.
This high symmetry has important implications in various fields, from crystallography to computer graphics, as we will explore later.
Dual Nature: The Relationship with the Cube
A fascinating aspect of the octahedron is its dual relationship with the cube. What does this mean? If you connect the centers of each face of a cube, you create an octahedron. Conversely, connecting the centers of the faces of an octahedron creates a cube. This duality showcases a beautiful interconnectedness between these two seemingly different shapes.
Platonic Solid: A Member of an Elite Group
The regular octahedron is one of the five Platonic solids. These are convex regular polyhedra, meaning all their faces are congruent regular polygons, and the same number of faces meet at each vertex. The other Platonic solids are the tetrahedron, cube, dodecahedron, and icosahedron. Each of these solids holds a unique position in geometry due to their perfect symmetry and mathematical elegance. Understanding the octahedron provides a deeper appreciation for this elite group of shapes.
Calculating Volume and Surface Area
For a regular octahedron with edge length 'a', the formulas for calculating its volume (V) and surface area (A) are as follows:
- Volume (V): V = (√2/3) * a³
- Surface Area (A): A = 2√3 * a²
These formulas allow for precise calculations of the octahedron's physical properties, making them essential tools in applications involving volume and surface area estimations.
Beyond the Regular Form: Irregular Octahedra
While the regular octahedron is the most commonly discussed, it’s crucial to remember that the term "octahedron" encompasses a broader category of shapes. Irregular octahedra exist, where the faces are still triangles but are not necessarily equilateral, and the edges are not all of equal length. These shapes lack the perfect symmetry of their regular counterpart but still adhere to the fundamental definition of having eight vertices and six faces.
Examples of irregular octahedra can be found in various natural formations and architectural designs where perfect symmetry isn't a requirement.
Applications of Octahedra: From Nature to Technology
The octahedron's unique properties have led to its appearance in diverse fields:
Crystallography: The Building Blocks of Minerals
Many minerals crystallize in octahedral forms. The inherent symmetry of the octahedron allows for efficient packing of atoms and molecules, resulting in stable and naturally occurring crystalline structures. This understanding is crucial in mineralogy and materials science.
Chemistry: Molecular Structures
Certain molecules exhibit octahedral geometry, where an atom is bonded to six other atoms, arranged at the vertices of an octahedron. This arrangement plays a significant role in the molecule's reactivity and properties.
Computer Graphics and Game Design: Creating Realistic Models
The octahedron's symmetrical nature makes it a valuable tool in computer graphics and game design. It can be used as a base for creating more complex 3D models, or as a component in procedural generation algorithms. Its inherent symmetry simplifies calculations and rendering processes.
Architecture and Design: Inspiration for Innovative Structures
The octahedron's strength and stability have inspired innovative architectural and engineering designs. Its symmetrical form allows for efficient distribution of forces, leading to structurally sound and aesthetically pleasing structures. While not always overtly obvious, the underlying principles of octahedral geometry influence modern design.
Games and Puzzles: Engaging Challenges
The octahedron's unique shape has been incorporated into various games and puzzles. The inherent spatial reasoning required to manipulate and understand this shape adds an extra layer of complexity and engagement.
Exploring Further: Related Geometric Concepts
Understanding the octahedron opens doors to exploring related concepts in geometry:
- Polyhedra: The octahedron belongs to a larger family of shapes called polyhedra, which are three-dimensional shapes with flat faces. Exploring different types of polyhedra expands one's understanding of geometric principles.
- Euler's Formula: Euler's formula, V - E + F = 2, relates the number of vertices (V), edges (E), and faces (F) of any convex polyhedron. The octahedron perfectly exemplifies this fundamental relationship in geometry (8 - 12 + 6 = 2).
- Stellations and Truncations: More complex shapes can be derived from the octahedron through stellation (adding pyramids to its faces) and truncation (cutting off its corners). These operations yield fascinating variations on the basic octahedral form, highlighting the versatility of this shape.
Conclusion: The Enduring Appeal of the Octahedron
The octahedron, with its eight vertices and six faces, is more than just a geometrical abstraction. It is a shape that seamlessly bridges the gap between theoretical mathematics and the practical world. Its inherent symmetry, dual relationship with the cube, and appearance in various natural and man-made contexts highlight its enduring significance. From crystal structures to computer graphics, the octahedron continues to fascinate and inspire, showcasing the beauty and power of geometric forms. Understanding this shape deepens one's appreciation for the intricate and often hidden patterns that govern the world around us. Exploring its properties and applications provides a valuable insight into the fascinating world of geometry and its far-reaching influences.
Latest Posts
Latest Posts
-
Drawing Of Law Of Conservation Of Mass
Apr 03, 2025
-
A Homogeneous Mixture Is Also Called A
Apr 03, 2025
-
A Substance Formed During A Chemical Reaction
Apr 03, 2025
-
Give The Major Product Of The Following Reaction
Apr 03, 2025
-
An Npn Transistor Is Made Up Of
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Whats A Shape With 8 Vertices And 6 Faces. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
