What The Square Root Of 30
Juapaving
Apr 05, 2025 · 5 min read
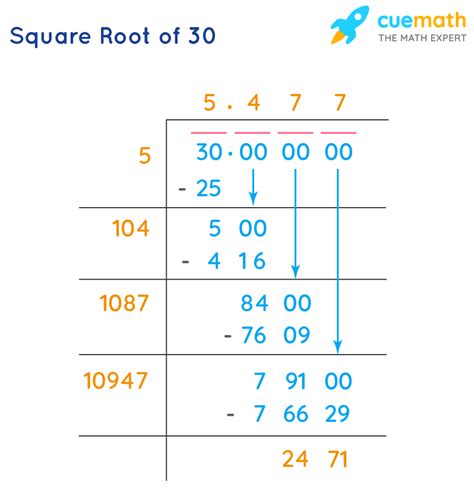
Table of Contents
What is the Square Root of 30? A Deep Dive into Irrational Numbers
The square root of 30, denoted as √30, is a fascinating mathematical concept that encapsulates the essence of irrational numbers. While seemingly simple at first glance, exploring its properties reveals a rich tapestry of mathematical ideas and applications. This article delves into the intricacies of √30, exploring its approximate value, its position within the number system, its calculation methods, and its significance in various fields.
Understanding Square Roots
Before we delve into the specifics of √30, let's establish a foundational understanding of square roots. A square root of a number x is a value that, when multiplied by itself, equals x. In simpler terms, it's the inverse operation of squaring a number. For instance, the square root of 9 (√9) is 3, because 3 multiplied by itself (3 x 3) equals 9.
The Irrational Nature of √30
Unlike the square root of 9, which yields a whole number, the square root of 30 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating, meaning it continues infinitely without ever settling into a repeating pattern. This characteristic distinguishes irrational numbers from rational numbers (which can be expressed as fractions). The irrationality of √30 stems from the fact that 30 is not a perfect square – it's not the product of any integer multiplied by itself.
Approximating the Value of √30
Since we cannot express √30 as an exact decimal, we rely on approximations. Using a calculator, we find that √30 is approximately 5.477225575. This value is a truncation, meaning we've cut off the infinitely long decimal expansion. Depending on the level of precision required, we can use a more or less precise approximation. For many practical applications, rounding to a few decimal places (e.g., 5.48) provides sufficient accuracy.
Methods for Calculating √30
Several methods exist for approximating the square root of 30. Let's explore a few:
1. Using a Calculator
The most straightforward method is to use a calculator or computer software equipped with a square root function. This provides a rapid and accurate approximation.
2. The Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to progressively closer approximations. The formula is:
x<sub>n+1</sub> = 0.5 * (x<sub>n</sub> + (30 / x<sub>n</sub>))
Where:
- x<sub>n</sub> is the current approximation
- x<sub>n+1</sub> is the next, improved approximation
Start with an initial guess (e.g., x<sub>0</sub> = 5), and repeatedly apply the formula. Each iteration yields a more accurate approximation. This method converges quite rapidly.
3. Newton-Raphson Method
This is another iterative method for finding successively better approximations to the roots of a real-valued function. For finding the square root of 30, we can use the function f(x) = x² - 30. The Newton-Raphson formula is:
x<sub>n+1</sub> = x<sub>n</sub> - f(x<sub>n</sub>) / f'(x<sub>n</sub>)
Where:
- f'(x<sub>n</sub>) is the derivative of f(x) at x<sub>n</sub> (which is 2x<sub>n</sub> in this case).
Similar to the Babylonian method, an initial guess is refined through repeated iterations.
4. Long Division Method
While less efficient than iterative methods, the long division method provides a way to manually calculate square roots to a desired level of precision. This method is quite involved and requires a good understanding of long division and its application to square root calculation.
√30 in Geometry and Other Applications
The square root of 30 has practical applications in various fields:
1. Geometry
Consider a right-angled triangle. If two of its legs have lengths a and b, and the hypotenuse (the side opposite the right angle) has length c, the Pythagorean theorem states:
a² + b² = c²
If we know the lengths of two sides, we can calculate the length of the third. If a = 3 and b = 5, then c² = 34. Therefore, c = √34. Similarly, various geometric problems might involve calculating lengths related to √30.
2. Physics
Many physics equations involve square roots. For instance, calculations involving velocity, energy, or distance might lead to expressions containing square roots of numbers. The specific context determines the significance of √30.
3. Engineering
In engineering design and calculations, square roots frequently arise. For instance, calculations involving stress, strain, or other physical quantities often involve expressions containing square roots.
√30 and its Position in the Number Line
√30 lies between the perfect squares √25 (which is 5) and √36 (which is 6). This places it on the number line between 5 and 6, closer to 5. Its exact position on the number line is irrational and cannot be precisely marked with a finite decimal representation.
The Significance of Irrational Numbers
The existence of irrational numbers like √30 highlights the richness and complexity of the number system. It underscores that not all numbers can be expressed as simple ratios, challenging the initial intuition of dealing solely with whole numbers and fractions. The discovery and understanding of irrational numbers expanded the horizons of mathematics, leading to further developments in geometry, calculus, and other advanced mathematical fields.
Conclusion: √30 and Beyond
The square root of 30, while seemingly a simple concept, embodies a deeper mathematical significance. Its irrationality underscores the complexities of the number system and provides a gateway to explore various calculation methods and applications within geometry, physics, and engineering. Understanding its properties enriches our mathematical understanding and demonstrates the practical relevance of irrational numbers in various scientific and technological domains. Further exploration into the fascinating world of irrational numbers reveals even greater mathematical depths. From simple approximations to sophisticated iterative methods, the journey of understanding √30 provides a solid foundation for delving into more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How Many Food Chains Make Up The Food Web
Apr 06, 2025
-
69 1 Liquid Measurement Ratio Calculator
Apr 06, 2025
-
Elements That Are Good Conductors Of Heat And Electricity Are
Apr 06, 2025
-
Which Of The Following Is Not A Property Of Bases
Apr 06, 2025
-
What Is Difference Between Gas And Vapour
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What The Square Root Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
