What Shape Has 6 Faces 8 Vertices And 12 Edges
Juapaving
Apr 01, 2025 · 5 min read
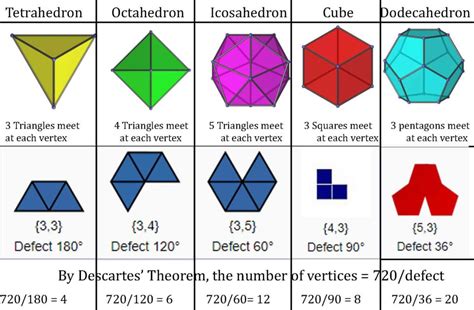
Table of Contents
What Shape Has 6 Faces, 8 Vertices, and 12 Edges? Unlocking the Mystery of the Cube
The question, "What shape has 6 faces, 8 vertices, and 12 edges?" might seem like a simple geometry puzzle. However, understanding the answer delves into the fascinating world of solid geometry, specifically focusing on Platonic solids and their unique properties. The answer, as we'll explore in detail, is a cube. But simply stating the answer doesn't do justice to the rich mathematical concepts involved. This article will not only reveal the answer but also explain why, exploring related concepts and providing further insights into the world of three-dimensional shapes.
Understanding the Terminology: Faces, Vertices, and Edges
Before diving into the solution, let's clarify the terminology:
- Faces: These are the flat surfaces of a three-dimensional shape. Think of them as the sides of a box.
- Vertices: These are the points where the edges of a shape meet. They are the corners of the shape.
- Edges: These are the line segments where two faces meet. They are the lines that form the boundaries of the faces.
Euler's Formula: A Fundamental Relationship
A crucial concept in understanding polyhedra (three-dimensional shapes with flat faces) is Euler's formula. This fundamental theorem establishes a relationship between the number of faces (F), vertices (V), and edges (E) of any convex polyhedron. The formula is:
F + V - E = 2
This formula holds true for all convex polyhedra, meaning shapes where any line segment connecting two points within the shape lies entirely within the shape. Let's verify this formula with the cube:
- Faces (F) = 6 (six square faces)
- Vertices (V) = 8 (eight corners)
- Edges (E) = 12 (twelve line segments)
Applying Euler's formula: 6 + 8 - 12 = 2. The formula holds true! This formula is a powerful tool for verifying the properties of polyhedra and helps in identifying shapes based on the number of faces, vertices, and edges.
Identifying the Shape: The Cube
Given the characteristics – 6 faces, 8 vertices, and 12 edges – we can confidently identify the shape as a cube. A cube is a special type of hexahedron (a six-sided polyhedron), characterized by its six square faces, all of which are congruent (identical in size and shape). Each vertex connects three edges, and each edge connects two faces. These are defining features of a cube.
Properties of a Cube: A Deeper Dive
The cube possesses several key properties that distinguish it from other three-dimensional shapes:
- Regularity: A cube is a regular polyhedron, meaning all its faces are identical regular polygons (in this case, squares), and all its vertices are congruent.
- Symmetry: The cube exhibits high levels of symmetry. It has rotational symmetry around various axes and reflectional symmetry across several planes.
- Volume and Surface Area: The volume and surface area of a cube can be easily calculated using simple formulas, making it a fundamental shape in various fields like engineering and architecture.
Distinguishing the Cube from Other Polyhedra
While the cube uniquely fits the given criteria of 6 faces, 8 vertices, and 12 edges, it's important to understand how it differs from other polyhedra:
- Rectangular Prisms: These also have 6 faces, 8 vertices, and 12 edges. However, unlike a cube, the faces of a rectangular prism are rectangles, not necessarily squares. A cube is a special case of a rectangular prism where all sides are equal.
- Other Polyhedra: Numerous other polyhedra exist with different combinations of faces, vertices, and edges. Euler's formula helps to constrain the possibilities, but unique characteristics of each shape determine its identity.
Applications of the Cube: Real-World Examples
The cube's simple yet robust geometry makes it ubiquitous in numerous applications:
- Architecture and Construction: Cubes and cuboid structures are fundamental in building design, offering stability and efficient use of space.
- Packaging and Logistics: Cubical boxes are standard packaging units, optimizing storage and transportation.
- Games and Puzzles: The cube forms the basis of various games and puzzles, such as Rubik's Cube, engaging problem-solving skills.
- Art and Design: The cube's geometric simplicity inspires artists and designers, appearing in sculptures, paintings, and architectural designs.
- Mathematics and Science: The cube serves as a fundamental shape in various mathematical and scientific models, from crystal structures to computer graphics.
Expanding the Knowledge: Exploring Other Platonic Solids
The cube is one of the five Platonic solids. These are regular convex polyhedra, possessing identical regular polygonal faces and congruent vertices. The other four are:
- Tetrahedron: 4 faces, 4 vertices, 6 edges
- Octahedron: 8 faces, 6 vertices, 12 edges
- Dodecahedron: 12 faces, 20 vertices, 30 edges
- Icosahedron: 20 faces, 12 vertices, 30 edges
Each of these Platonic solids exhibits unique properties and applications, expanding our understanding of three-dimensional geometry.
Conclusion: The Cube's Enduring Significance
In conclusion, the shape with 6 faces, 8 vertices, and 12 edges is a cube. Understanding this seemingly simple answer requires delving into the fundamental principles of solid geometry, including Euler's formula and the properties of regular polyhedra. The cube's significance extends far beyond its geometric definition, impacting various fields and inspiring countless applications. Exploring this seemingly simple shape unveils a rich tapestry of mathematical concepts and real-world significance, highlighting the beauty and power of geometry. By applying Euler's formula and understanding the unique characteristics of the cube, we can accurately identify and appreciate its importance in various aspects of life. This exploration emphasizes the importance of applying mathematical principles to real-world scenarios and the enduring influence of geometric shapes in our understanding of the world around us. From architecture to puzzles, the humble cube continues to inspire and intrigue. The journey of understanding this shape underlines the fascinating intersection of mathematics and the physical world.
Latest Posts
Latest Posts
-
What Are The Chanses Of Getting Two
Apr 02, 2025
-
Period 1 Contains A Total Of Elements
Apr 02, 2025
-
Which Statements Are True Regarding Undefinable Terms In Geometry
Apr 02, 2025
-
What Is 3 Of 1 Million
Apr 02, 2025
-
In What Cell Organelle Does Photosynthesis Occur
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Shape Has 6 Faces 8 Vertices And 12 Edges . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
