What Percentage Is 2 Of 6
Juapaving
May 12, 2025 · 4 min read
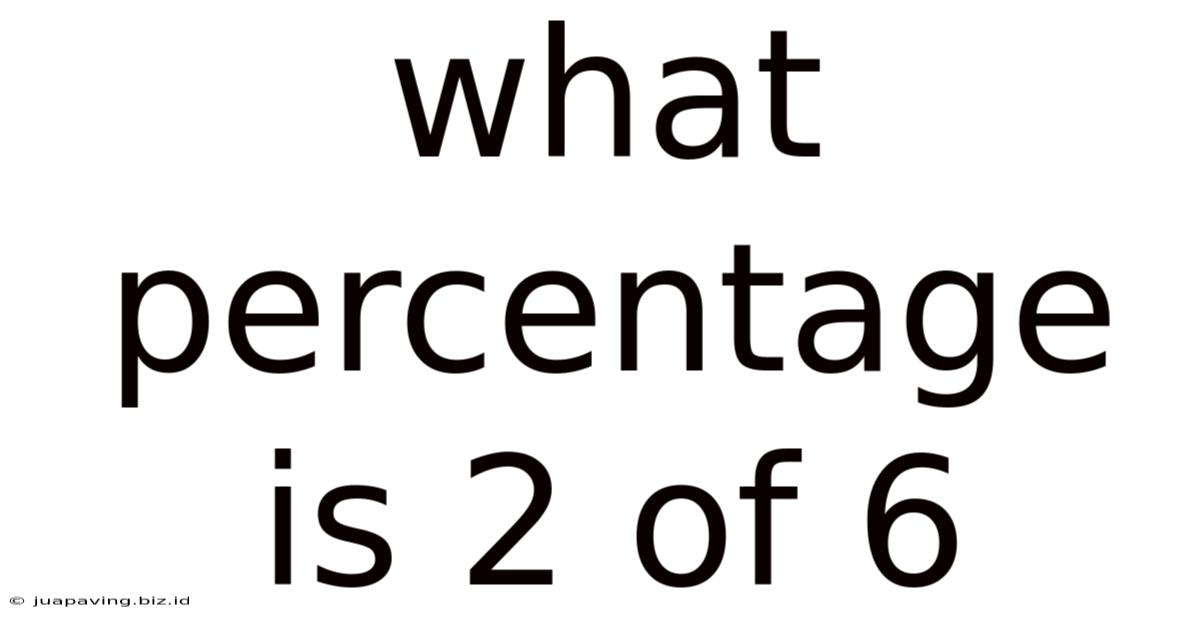
Table of Contents
What Percentage is 2 of 6? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide delves into the question, "What percentage is 2 of 6?", providing a detailed explanation of the calculation, practical applications, and related percentage concepts. We'll explore different methods of solving this problem and offer insights into how to tackle similar percentage calculations confidently.
Understanding the Basics of Percentages
Before we dive into calculating the percentage, let's establish a solid understanding of what a percentage represents. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Key Terms:
- Part: The number you are comparing (in this case, 2).
- Whole: The total number you are comparing against (in this case, 6).
- Percentage: The ratio of the part to the whole, expressed as a number out of 100.
Calculating the Percentage: What Percentage is 2 of 6?
There are several ways to calculate what percentage 2 is of 6. Let's explore the most common methods:
Method 1: Using the Formula
The standard formula for calculating percentages is:
(Part / Whole) * 100%
Substituting our values:
(2 / 6) * 100% = 0.3333... * 100% ≈ 33.33%
Therefore, 2 is approximately 33.33% of 6.
Method 2: Simplifying the Fraction
We can simplify the fraction 2/6 before multiplying by 100%. Both 2 and 6 are divisible by 2:
2/6 = 1/3
Now, we can convert the fraction 1/3 to a percentage:
(1 / 3) * 100% ≈ 33.33%
This method offers a slightly simpler calculation.
Method 3: Using Proportions
We can set up a proportion to solve this problem:
2/6 = x/100
To solve for x (the percentage), we cross-multiply:
6x = 200
x = 200/6 ≈ 33.33%
This method reinforces the concept of equivalent ratios.
Understanding the Result: 33.33%
The result, 33.33%, indicates that 2 represents approximately one-third (1/3) of 6. This percentage is recurring, meaning the decimal part (0.3333...) continues infinitely. For practical purposes, rounding to two decimal places (33.33%) is usually sufficient.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
1. Sales and Discounts:
Imagine a shirt originally priced at $6 is on sale for $2. Using the percentage calculation, you can quickly determine that the discount is 33.33%.
2. Financial Analysis:
Percentage calculations are essential in analyzing financial data, such as calculating profit margins, interest rates, and investment returns. Understanding the percentage change in sales or profits over time is crucial for business decision-making.
3. Data Analysis and Statistics:
Percentages are extensively used in statistics to represent proportions, such as the percentage of a population with a specific characteristic or the percentage of successful outcomes in an experiment.
4. Everyday Life:
From calculating tips at restaurants to understanding sales tax, percentage calculations are used frequently in everyday situations.
Further Exploring Percentage Concepts
Let's delve deeper into related percentage concepts that build upon our understanding of this calculation:
1. Percentage Increase and Decrease:
Understanding how to calculate percentage increases and decreases is crucial for analyzing changes in values. For example, if a value increases from 6 to 8, the percentage increase is calculated as follows:
[(8 - 6) / 6] * 100% = 33.33%
Similarly, a decrease from 6 to 4 would result in a 33.33% decrease.
2. Percentage Points vs. Percentage Change:
It's essential to differentiate between percentage points and percentage change. Percentage points represent the absolute difference between two percentages, while percentage change represents the relative difference. For instance, an increase from 20% to 25% is a 5 percentage point increase but a 25% percentage change.
3. Calculating the Whole when the Percentage and Part are Known:
Sometimes, you might know the percentage and the part and need to calculate the whole. For example, if 33.33% of a number is 2, you can set up the following equation:
(33.33/100) * x = 2
Solving for x (the whole), we get x ≈ 6.
Mastering Percentage Calculations: Tips and Tricks
Here are some tips to improve your skills in percentage calculations:
- Practice Regularly: Consistent practice is key to mastering any mathematical concept. Solve various percentage problems to build your confidence and speed.
- Understand the Concepts: A strong understanding of the underlying concepts is crucial. Focus on understanding the formula and its application in different contexts.
- Use a Calculator: While manual calculations are beneficial for understanding the process, a calculator can streamline the process, especially with more complex calculations.
- Break Down Complex Problems: When faced with complex percentage problems, break them down into smaller, manageable steps.
- Check Your Work: Always double-check your calculations to ensure accuracy.
Conclusion: Confidence in Percentage Calculations
Understanding percentage calculations, such as determining "What percentage is 2 of 6?", is a valuable skill applicable in numerous scenarios. By mastering the different methods presented in this guide, you can confidently tackle similar percentage problems and apply your knowledge to various practical applications. Remember that consistent practice and a solid understanding of the underlying concepts are key to building your expertise. With enough practice, percentage calculations will become second nature.
Latest Posts
Latest Posts
-
What Is Gcf Of 12 And 15
May 12, 2025
-
Are Opposite Angles Of A Parallelogram Equal
May 12, 2025
-
How Many Lines Of Symmetry Does A Rectangular Pentagon Have
May 12, 2025
-
An Electrical Conductor Is A Material That Allows
May 12, 2025
-
What Happens When A Mature Spirogyra Filament Attains Considerable Length
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 2 Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.