What Is Gcf Of 12 And 15
Juapaving
May 12, 2025 · 6 min read
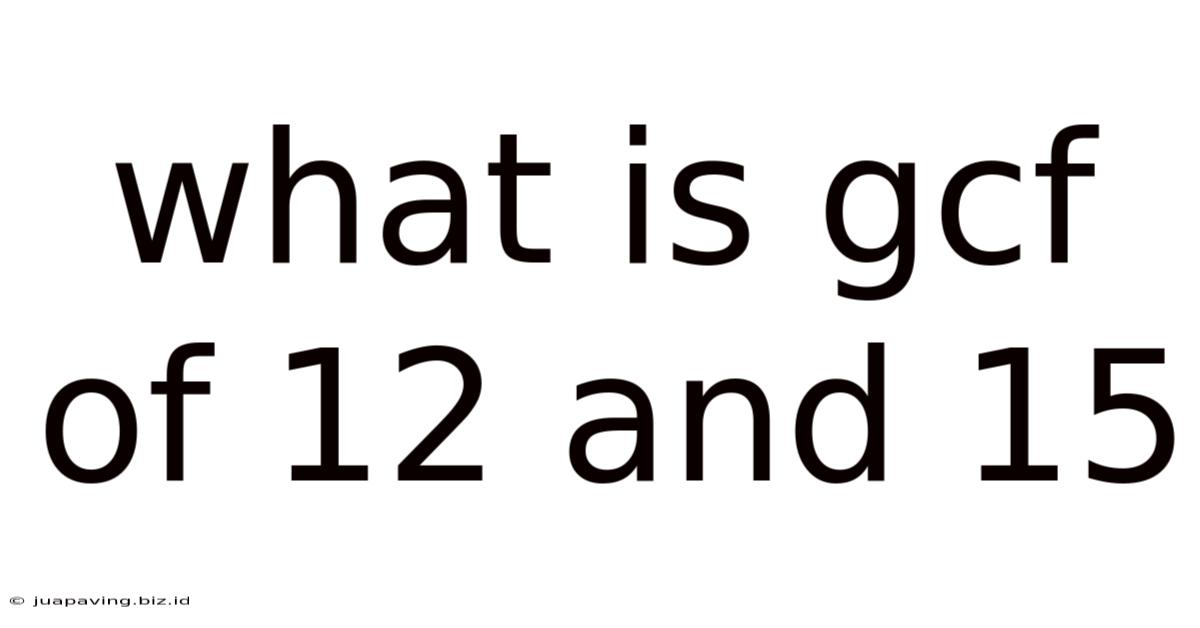
Table of Contents
What is the GCF of 12 and 15? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the concept thoroughly unlocks a world of mathematical possibilities. This in-depth guide will not only answer the question, "What is the GCF of 12 and 15?" but also explore the underlying principles, different methods for finding the GCF, and its applications in various mathematical contexts.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can be evenly divided into both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding number theory.
Why is the GCF Important?
The GCF plays a crucial role in various mathematical operations:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. By dividing both the numerator and denominator by their GCF, we obtain an equivalent fraction in its simplest form. For example, simplifying 12/15 requires finding the GCF of 12 and 15.
-
Algebraic Expressions: The GCF is vital in factoring algebraic expressions. Finding the GCF of the terms allows us to rewrite the expression in a more concise and manageable form.
-
Number Theory: The GCF is a cornerstone of number theory, a branch of mathematics that studies the properties of integers. Concepts like relatively prime numbers (numbers with a GCF of 1) and the Euclidean algorithm (a method for finding the GCF) are fundamental to number theory.
-
Real-World Applications: While seemingly abstract, the GCF finds practical applications in areas like dividing objects into equal groups, determining the dimensions of objects, and solving problems involving ratios and proportions.
Finding the GCF of 12 and 15: Multiple Methods
There are several methods to determine the greatest common factor of two numbers. Let's explore the most common approaches, applying them to find the GCF of 12 and 15.
Method 1: Listing Factors
This method involves listing all the factors of each number and identifying the largest factor common to both.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 15: 1, 3, 5, 15
The common factors of 12 and 15 are 1 and 3. Therefore, the GCF of 12 and 15 is 3.
Method 2: Prime Factorization
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
Prime factorization of 12: 2² x 3 Prime factorization of 15: 3 x 5
The only common prime factor is 3 (both numbers have at least one 3). Therefore, the GCF of 12 and 15 is 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a more efficient method for finding the GCF of larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
- Start with the two numbers: 12 and 15.
- Subtract the smaller number from the larger: 15 - 12 = 3
- Now we have 12 and 3.
- Subtract the smaller number from the larger: 12 - 3 = 9
- Now we have 9 and 3.
- Subtract the smaller number from the larger: 9 - 3 = 6
- Now we have 6 and 3.
- Subtract the smaller number from the larger: 6-3 =3
- Now we have 3 and 3. The numbers are equal.
Therefore, the GCF of 12 and 15 is 3.
A more efficient version of the Euclidean Algorithm involves successive division instead of subtraction. We repeatedly divide the larger number by the smaller number and replace the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCF.
- Divide 15 by 12: 15 = 12 x 1 + 3 (remainder is 3)
- Divide 12 by 3: 12 = 3 x 4 + 0 (remainder is 0)
The last non-zero remainder is 3. Therefore, the GCF of 12 and 15 is 3.
Beyond the Basics: Extending the GCF Concept
The concept of GCF extends beyond just two numbers. We can find the GCF of three or more numbers using the same principles. For example, to find the GCF of 12, 15, and 18:
-
Prime Factorization Method:
- 12 = 2² x 3
- 15 = 3 x 5
- 18 = 2 x 3²
The common prime factor is 3 (each number contains at least one factor of 3). Therefore, the GCF of 12, 15, and 18 is 3.
-
Euclidean Algorithm (for multiple numbers): The Euclidean algorithm can be extended to multiple numbers by iteratively finding the GCF of pairs of numbers. For instance:
- Find the GCF of 12 and 15 (which is 3).
- Then find the GCF of 3 and 18 (which is 3). Therefore the GCF of 12, 15 and 18 is 3.
Applications of GCF in Real-World Scenarios
The concept of the greatest common factor isn't confined to the realm of abstract mathematics. It has practical applications in various everyday situations:
-
Dividing Objects into Equal Groups: Imagine you have 12 apples and 15 oranges. You want to divide them into equal groups, with each group having the same number of apples and oranges. The GCF (3) tells you that you can create 3 equal groups, each containing 4 apples and 5 oranges.
-
Simplifying Ratios and Proportions: Ratios and proportions often need simplification. Finding the GCF helps reduce the ratio to its simplest form. For example, a ratio of 12:15 can be simplified to 4:5 by dividing both numbers by their GCF (3).
-
Geometry and Measurements: The GCF is useful when determining the dimensions of objects or determining the largest possible square tile that can evenly cover a rectangular area.
Conclusion: Mastering the GCF
Understanding the greatest common factor is crucial for various mathematical operations and practical applications. Whether you use the listing factors method, prime factorization, or the Euclidean algorithm, finding the GCF is a fundamental skill that simplifies calculations and offers valuable insights into number relationships. The GCF of 12 and 15, as demonstrated through multiple methods, is 3. This seemingly simple concept lays the groundwork for more advanced mathematical explorations. Remember to practice these methods to build proficiency and to tackle more complex GCF problems with ease. Mastering the GCF opens doors to a deeper understanding of number theory and its relevance in the real world.
Latest Posts
Latest Posts
-
What Does Origin And Insertion Mean In Anatomy
May 12, 2025
-
What Percentage Is 100 Of 500
May 12, 2025
-
The Atomic Mass Number Is Equal To
May 12, 2025
-
Comparing Prokaryotic And Eukaryotic Cells Venn Diagram
May 12, 2025
-
Are Humans Mammals Yes Or No
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is Gcf Of 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.