What Is True About Irrational Numbers
Juapaving
Apr 01, 2025 · 6 min read
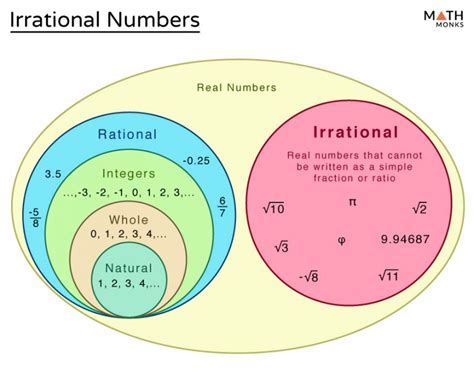
Table of Contents
What's Truly Irrational About Irrational Numbers? A Deep Dive
Irrational numbers. The very name conjures up a sense of mystery and perhaps, a little fear. They're the numbers that seem to defy logic, the rebels of the mathematical world, forever refusing to be neatly expressed as a simple fraction. But what exactly is true about these enigmatic entities? Let's unravel the mysteries surrounding irrational numbers, exploring their properties, significance, and the fascinating history behind their discovery.
Defining the Irrational: Beyond Fractions
At its core, an irrational number is any real number that cannot be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. This simple definition encapsulates the essence of their irrationality: they cannot be represented as a ratio of two whole numbers. This seemingly straightforward definition opens the door to a world of mathematical intricacies.
The Contrast with Rational Numbers
To fully grasp the concept of irrational numbers, it's helpful to contrast them with their counterparts, rational numbers. Rational numbers, as the name suggests, are numbers that can be expressed as a ratio of two integers. This includes:
- Integers: Whole numbers, both positive and negative (e.g., -3, 0, 5).
- Fractions: Numbers expressed as a ratio of two integers (e.g., 1/2, -3/4, 7/1).
- Terminating Decimals: Decimals that end after a finite number of digits (e.g., 0.75, 2.5, 0.125).
- Repeating Decimals: Decimals with a pattern of digits that repeats infinitely (e.g., 0.333..., 0.142857142857...).
The key difference lies in the ability to represent the number as a fraction. Rational numbers can; irrational numbers cannot.
Famous Irrational Numbers: Pi, e, and the Golden Ratio
Several irrational numbers hold significant importance in mathematics and science. These include:
1. Pi (π)
Perhaps the most famous irrational number is Pi (π), the ratio of a circle's circumference to its diameter. It's approximately 3.14159, but its decimal representation continues infinitely without repeating. Pi's ubiquity in geometry, trigonometry, and calculus makes it a cornerstone of mathematics. Its irrationality was proven centuries ago, highlighting the inherent complexity within seemingly simple geometric shapes.
2. Euler's Number (e)
Euler's number (e), approximately 2.71828, is another fundamental irrational constant. It arises naturally in calculus, particularly in exponential functions and growth calculations. Its irrationality underscores the complexities inherent in continuous growth models and the subtle nature of exponential functions. The constant appears in many areas of science and engineering, further emphasizing its importance.
3. The Golden Ratio (φ)
The Golden Ratio (φ), approximately 1.61803, is a fascinating irrational number found in geometry, art, and nature. It's defined as the ratio of a line cut into two segments so that the ratio of the whole segment to the longer segment equals the ratio of the longer segment to the shorter segment. Its presence in the proportions of the Great Pyramid of Giza, the Parthenon, and even in the arrangement of sunflower seeds speaks to its deep-rooted mathematical significance and aesthetically pleasing properties. Its irrationality adds another layer of intrigue to its many appearances.
Proving Irrationality: A Mathematical Challenge
Proving a number is irrational can be a significant mathematical undertaking. The proofs often involve techniques of contradiction and a deep understanding of number theory. Here's a glimpse into the logic involved:
-
Proof by Contradiction: This is a common method. One assumes the number is rational (can be expressed as a fraction), then demonstrates that this assumption leads to a logical contradiction. This contradiction proves the initial assumption was false, thereby establishing the number's irrationality.
-
Unique Prime Factorization: This fundamental theorem of arithmetic plays a crucial role in many irrationality proofs. It states that every integer greater than 1 can be uniquely factored into a product of prime numbers. This property is often exploited to show inconsistencies if a number is assumed to be rational.
The Significance of Irrational Numbers
The existence of irrational numbers fundamentally altered our understanding of numbers and mathematics. They demonstrated that:
-
The number line is dense: Between any two rational numbers, there exists an infinite number of irrational numbers. This highlights the richness and complexity of the real number system.
-
Geometric constructions have limitations: Certain geometric constructions, such as squaring the circle (constructing a square with the same area as a given circle using only a compass and straightedge), were proven impossible due to the irrationality of π. This had profound implications for classical geometry.
-
Mathematical models are refined: The use of irrational numbers enhances the accuracy and precision of mathematical models in various scientific and engineering applications. Using rational approximations, while sometimes practical, sacrifices accuracy for convenience. The use of irrational constants like e and π allows for more precise calculations and predictions in numerous fields.
-
Infinite non-repeating decimals: The discovery and understanding of irrational numbers greatly expanded our comprehension of the nature of numbers themselves. It challenged the earlier assumptions that all numbers could be neatly expressed as ratios and opened the door to a more nuanced and expansive view of the mathematical universe.
Implications in Different Fields
Irrational numbers aren't just abstract mathematical concepts; they have tangible implications in various fields:
-
Physics: Irrational numbers frequently appear in physical laws and constants, such as the fine-structure constant in quantum electrodynamics. This constant, an irrational number, governs the strength of the electromagnetic interaction between elementary charged particles. Accurate calculations in these fields necessitate the use and understanding of irrational numbers.
-
Engineering: In engineering design and construction, precise calculations involving irrational numbers, such as π in calculating the circumference of a pipe or the surface area of a sphere, are vital for accuracy and efficiency. The implications of even small inaccuracies can be significant in large-scale projects.
-
Computer Science: Irrational numbers present computational challenges. Representing irrational numbers precisely in computer systems requires approximations using floating-point numbers, which introduces potential rounding errors. Understanding these errors and their propagation is crucial for ensuring the accuracy of computations.
-
Finance: Compound interest calculations, crucial in finance, involve exponential functions which inherently utilize the irrational constant e. Accurate financial modeling and forecasting require incorporating the nuances of these exponential functions and the implications of the irrational constant.
Beyond the Basics: Deeper Explorations
The world of irrational numbers extends far beyond the basic definitions and examples. There are many deeper concepts and areas of exploration, including:
-
Transcendental Numbers: A subset of irrational numbers, transcendental numbers are those that are not roots of any non-zero polynomial equation with rational coefficients. Both e and π are transcendental numbers, a fact that has profound implications in various branches of mathematics.
-
Liouville Numbers: These are irrational numbers that can be approximated unusually well by rational numbers. Their existence highlights the intricate relationships between rational and irrational numbers.
-
Continued Fractions: Irrational numbers can be represented as continued fractions, which offer a unique and often insightful way to express and analyze their properties.
Conclusion: The Enduring Enigma
Irrational numbers, far from being mere mathematical oddities, are fundamental building blocks of our mathematical understanding. Their existence challenges intuitive notions about numbers, forces us to grapple with infinity, and leads to deeper insights into the structure of the real number system. Their ubiquitous presence in various scientific and engineering fields demonstrates their practical significance, shaping our world in subtle but profound ways. The continuing exploration of irrational numbers remains a vibrant and rewarding area of mathematical research, promising new discoveries and a continually evolving understanding of these fascinating numbers.
Latest Posts
Latest Posts
-
Plant Is Where Photosynthesis Takes Place
Apr 02, 2025
-
12 Cm Is How Many Inches
Apr 02, 2025
-
The Most Abundant Gas In The Earths Atmosphere Is
Apr 02, 2025
-
Is Rubbing Alcohol And Denatured Alcohol The Same
Apr 02, 2025
-
Is 17 A Prime Number Or A Composite Number
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is True About Irrational Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
