What Is The Square Root 72
Juapaving
Mar 30, 2025 · 4 min read
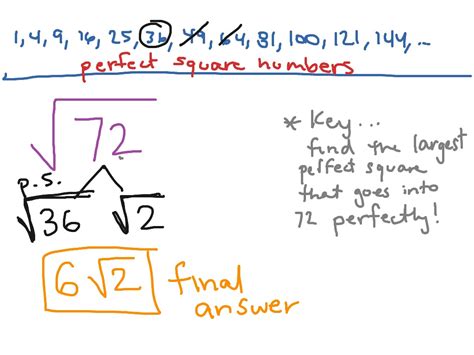
Table of Contents
What is the Square Root of 72? A Deep Dive into Simplification and Approximation
The question, "What is the square root of 72?" seems simple enough, but it opens the door to a fascinating exploration of mathematical concepts, including prime factorization, simplification of radicals, and different methods of approximation. This article will delve into each of these aspects, providing a comprehensive understanding of this seemingly straightforward problem.
Understanding Square Roots
Before tackling the square root of 72, let's establish a firm foundation. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. This is also known as finding a number's principal square root – there is also a negative counterpart, but for this exploration, we will focus on the positive value.
Prime Factorization: The Key to Simplification
The most effective method for simplifying the square root of 72 involves prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves.
Let's apply this to 72:
72 = 2 x 36 36 = 2 x 18 18 = 2 x 9 9 = 3 x 3
Therefore, the prime factorization of 72 is 2 x 2 x 2 x 3 x 3, or 2³ x 3².
Simplifying the Square Root of 72
Now that we have the prime factorization, we can simplify √72. Remember that √(a x a) = a. We can rewrite √72 using our prime factorization:
√72 = √(2 x 2 x 2 x 3 x 3)
We can group pairs of identical factors:
√72 = √(2 x 2) x √(3 x 3) x √2
Simplifying the pairs:
√72 = 2 x 3 x √2
Therefore, the simplified form of √72 is 6√2. This is the exact value, expressed in its simplest radical form. It means that 6 multiplied by the square root of 2 will give you 72.
Approximating the Square Root of 72
While 6√2 is the exact answer, it's not always practical. Sometimes, we need a numerical approximation. There are several methods to achieve this:
1. Using a Calculator
The simplest method is using a calculator. Most calculators have a square root function (√). Simply enter 72 and press the square root button. You'll get an approximation like 8.485.
2. Estimation
We can estimate the square root by considering perfect squares near 72. We know that 8² = 64 and 9² = 81. Since 72 is closer to 81 than to 64, we can estimate √72 to be slightly less than 9. This gives us a rough approximation.
3. Babylonian Method (or Heron's Method)
The Babylonian method is an iterative algorithm that refines an initial guess to obtain a closer approximation. The formula is:
x_(n+1) = 0.5 * (x_n + (N / x_n))
Where:
- x_n is the current approximation
- x_(n+1) is the next approximation
- N is the number whose square root is being calculated (72 in this case)
Let's start with an initial guess of 8:
- x_1 = 8
- x_2 = 0.5 * (8 + (72 / 8)) = 8.5
- x_3 = 0.5 * (8.5 + (72 / 8.5)) ≈ 8.485
As you can see, after just a few iterations, we get a very close approximation to the calculator's result.
4. Taylor Series Expansion
For those familiar with calculus, the Taylor series expansion can be used to approximate the square root. This involves using an infinite series to represent the function, but truncating it after a certain number of terms for an approximation. This method is more complex than the others mentioned but provides a high degree of accuracy.
Applications of Square Roots
Understanding square roots is crucial in many areas, including:
- Geometry: Calculating the length of the hypotenuse of a right-angled triangle using the Pythagorean theorem (a² + b² = c²).
- Physics: Solving problems related to distance, speed, and time.
- Engineering: Designing structures and calculating forces.
- Computer graphics: Transforming coordinates and performing calculations related to 2D and 3D shapes.
- Statistics: Calculating standard deviation and variance.
Beyond the Basics: Exploring Further
While we've covered the fundamental aspects of finding the square root of 72, the mathematical concepts involved extend far beyond this specific problem. Exploring topics like complex numbers (which include the square roots of negative numbers), different number systems, and advanced numerical methods will provide a deeper and more comprehensive mathematical understanding. The seemingly simple question of “What is the square root of 72?” serves as a gateway to a rich and rewarding exploration of mathematics.
Conclusion
The square root of 72, simplified, is 6√2. While a calculator can easily provide a numerical approximation (approximately 8.485), understanding the process of prime factorization and simplification is crucial for a true grasp of the mathematical concept. Whether you're using a calculator, estimating, employing the Babylonian method, or utilizing more advanced techniques, the ability to find and understand the square root is an essential skill in various fields. Remember that the exact value is the most accurate, but approximations are often necessary and useful in practical applications. The journey to understanding √72 has illuminated the broader world of mathematical exploration, showcasing the beauty and utility of seemingly simple problems.
Latest Posts
Latest Posts
-
Adjective That Starts With L To Describe A Mom
Apr 01, 2025
-
Is 35 A Multiple Of 6
Apr 01, 2025
-
Exponents Worksheets Pdf With Answers 7th
Apr 01, 2025
-
Is Chlorine A Pure Substance Or Mixture
Apr 01, 2025
-
How Do You Write 19 In Roman Numerals
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
