What Is The Solution Of This Linear System
Juapaving
Apr 02, 2025 · 6 min read
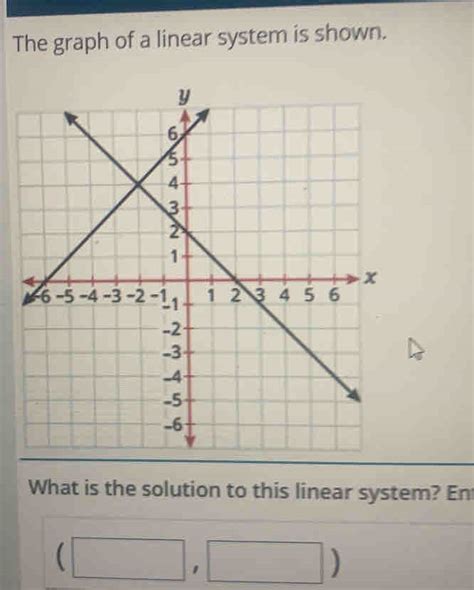
Table of Contents
Deciphering the Solution to a Linear System: A Comprehensive Guide
Solving linear systems is a fundamental concept in mathematics with wide-ranging applications across various fields, from engineering and physics to economics and computer science. This article provides a comprehensive guide to understanding and solving linear systems, exploring different methods and their applicability. We'll delve deep into the nuances of finding solutions, including scenarios with unique solutions, infinite solutions, and no solutions at all.
What is a Linear System?
A linear system is a collection of two or more linear equations involving the same set of variables. A linear equation is an equation where the highest power of each variable is 1. For instance:
- 2x + 3y = 7
- x - y = 1
This is a system of two linear equations with two variables (x and y). The goal is to find the values of x and y that satisfy both equations simultaneously. These values represent the solution to the linear system. The number of equations and variables can vary, leading to systems of different sizes and complexities.
Methods for Solving Linear Systems
Several methods exist for solving linear systems. The choice of method often depends on the size and structure of the system. The most common methods include:
1. Elimination Method (or Gaussian Elimination)
This method involves systematically eliminating variables from the equations until a single equation with a single variable remains. This can then be solved directly, and the solution can be back-substituted into previous equations to find the values of the other variables.
Example:
Let's solve the system:
- 2x + 3y = 7 (Equation 1)
- x - y = 1 (Equation 2)
- Multiply Equation 2 by 2: 2x - 2y = 2
- Subtract the modified Equation 2 from Equation 1: (2x + 3y) - (2x - 2y) = 7 - 2 => 5y = 5 => y = 1
- Substitute y = 1 into Equation 2: x - 1 = 1 => x = 2
Therefore, the solution is x = 2, y = 1.
2. Substitution Method
This method involves solving one equation for one variable in terms of the other variable(s) and then substituting this expression into the other equation(s). This reduces the number of variables and allows for a simpler solution.
Example: Using the same system as above:
- Solve Equation 2 for x: x = y + 1
- Substitute this expression for x into Equation 1: 2(y + 1) + 3y = 7
- Solve for y: 2y + 2 + 3y = 7 => 5y = 5 => y = 1
- Substitute y = 1 back into x = y + 1: x = 1 + 1 => x = 2
Again, the solution is x = 2, y = 1.
3. Graphical Method
This method involves plotting each equation on a graph. The point where the lines intersect represents the solution to the system. This method is visually intuitive but can be less accurate for complex systems or when solutions involve non-integer values.
Example: Plotting the two lines 2x + 3y = 7 and x - y = 1 will reveal their intersection point at (2, 1).
4. Matrix Methods
For larger systems of equations, matrix methods are significantly more efficient. These involve representing the system as a matrix equation (AX = B), where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix. Solutions can be found using techniques like:
-
Gaussian Elimination (Row Reduction): This is a systematic method of transforming the augmented matrix [A|B] into row-echelon form or reduced row-echelon form to solve for the variables.
-
Inverse Matrix Method: If the coefficient matrix A is invertible (has a non-zero determinant), the solution can be found directly as X = A⁻¹B, where A⁻¹ is the inverse of matrix A. This method is computationally expensive for large matrices.
Types of Solutions
A linear system can have one of three types of solutions:
1. Unique Solution:
This is the most common case where the system has exactly one solution. The lines (in a two-variable system) intersect at a single point, representing the unique values of the variables that satisfy all equations.
2. Infinite Solutions:
This occurs when the equations are linearly dependent, meaning one equation is a multiple of another. Geometrically, in a two-variable system, this means the lines are coincident (overlap completely). Any point on the line represents a solution.
3. No Solution:
This occurs when the equations are inconsistent, meaning there are no values of the variables that can satisfy all equations simultaneously. Geometrically, in a two-variable system, this means the lines are parallel and never intersect.
Identifying the Type of Solution
The type of solution can be determined during the solution process. For example, in the elimination or substitution method:
- Unique Solution: You will obtain unique values for each variable.
- Infinite Solutions: You will arrive at an equation that is always true (e.g., 0 = 0), indicating linear dependence.
- No Solution: You will arrive at an equation that is always false (e.g., 0 = 5), indicating inconsistency.
In matrix methods, the determinant of the coefficient matrix plays a crucial role:
- Unique Solution: The determinant is non-zero.
- Infinite Solutions: The determinant is zero, and there are free variables (variables that can take on any value).
- No Solution: The determinant is zero, and there is a contradiction in the reduced row-echelon form.
Applications of Linear Systems
The ability to solve linear systems is essential in numerous fields:
- Engineering: Analyzing circuits, structural mechanics, and control systems.
- Physics: Solving problems in mechanics, electromagnetism, and thermodynamics.
- Economics: Modeling market equilibrium, input-output analysis, and linear programming.
- Computer Science: Computer graphics, image processing, and machine learning algorithms.
- Chemistry: Solving stoichiometry problems and analyzing chemical reactions.
- Finance: Portfolio optimization and financial modeling.
Solving linear systems is a cornerstone of many mathematical models and computational techniques. Understanding the different methods and the potential types of solutions is crucial for effectively applying these tools in diverse areas.
Advanced Topics
For more advanced applications, consider exploring these topics:
- Linear Programming: Optimization problems involving linear objective functions and constraints.
- Systems of Non-linear Equations: Methods for solving equations where the variables are not raised to the power of 1.
- Numerical Methods for Linear Systems: Techniques for solving large or ill-conditioned linear systems using computational approaches.
This comprehensive guide provides a strong foundation for understanding and solving linear systems. Mastering these techniques opens doors to numerous applications across various disciplines, empowering you to model and solve complex problems effectively. The choice of method depends on the specific problem and the size of the system. Remember to always check your solutions and consider the type of solution possible—a unique solution, infinitely many solutions, or no solution at all. Through practice and understanding, you can become proficient in this fundamental mathematical skill.
Latest Posts
Latest Posts
-
What Percent Is 32 Of 40
Apr 03, 2025
-
Kindergarten Words That Begin With X
Apr 03, 2025
-
Examples Of Rays In Real Life
Apr 03, 2025
-
What Is The Prime Factorization Of 90
Apr 03, 2025
-
The Integuments Of The Ovule Develop Into The
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Solution Of This Linear System . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
