What Is The Smallest Multiple Of 3 And 4
Juapaving
Mar 26, 2025 · 5 min read
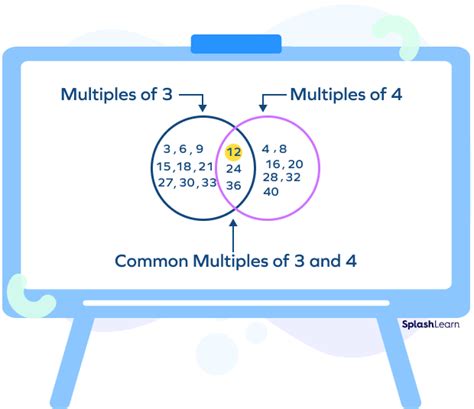
Table of Contents
What is the Smallest Multiple of 3 and 4? A Deep Dive into Least Common Multiples (LCM)
Finding the smallest multiple of 3 and 4 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward question opens the door to understanding fundamental mathematical concepts with far-reaching applications. This exploration will delve into the solution, explain the underlying principles, and illustrate how this concept extends to more complex scenarios.
Understanding Multiples
Before tackling the specific problem, let's solidify our understanding of multiples. A multiple of a number is the product of that number and any integer (whole number). For instance:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30... (3 x 1, 3 x 2, 3 x 3, and so on)
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40... (4 x 1, 4 x 2, 4 x 3, and so on)
Notice that some numbers appear in both lists. These are the common multiples of 3 and 4.
Identifying Common Multiples
The common multiples of 3 and 4 are the numbers that are divisible by both 3 and 4 without leaving a remainder. From the lists above, we can already see some: 12, 24, 36, and so on.
The Least Common Multiple (LCM)
The question asks for the smallest multiple of 3 and 4. This is formally known as the Least Common Multiple (LCM). The LCM is the smallest positive integer that is a multiple of all the numbers in a given set. In our case, the set is {3, 4}.
Finding the LCM: Method 1 - Listing Multiples
The most straightforward method, especially for small numbers, is to list the multiples of each number until a common multiple is found. As demonstrated earlier, the first common multiple of 3 and 4 is 12. Therefore, the LCM(3, 4) = 12.
Finding the LCM: Method 2 - Prime Factorization
A more efficient method, particularly useful for larger numbers, is prime factorization. This involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 3: 3 (3 is itself a prime number)
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization:
- List the prime factors of each number: We have 2² and 3.
- Take the highest power of each prime factor: The highest power of 2 is 2², and the highest power of 3 is 3¹.
- Multiply the highest powers together: 2² x 3 = 4 x 3 = 12
Therefore, the LCM(3, 4) = 12 using the prime factorization method.
Finding the LCM: Method 3 - Greatest Common Divisor (GCD) Method
Another approach involves using the Greatest Common Divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder. The relationship between LCM and GCD is expressed by the formula:
LCM(a, b) = (a x b) / GCD(a, b)
Let's apply this to our problem:
- Find the GCD of 3 and 4: The only common divisor of 3 and 4 is 1. Therefore, GCD(3, 4) = 1.
- Apply the formula: LCM(3, 4) = (3 x 4) / 1 = 12
This confirms, once again, that the LCM(3, 4) = 12.
Real-World Applications of LCM
The concept of the Least Common Multiple is not confined to abstract mathematical exercises. It has practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a stop, one every 3 minutes and the other every 4 minutes. The LCM helps determine when both buses will arrive simultaneously – every 12 minutes.
-
Construction and Engineering: In construction projects, materials might need to be cut into specific lengths, requiring the use of LCM to minimize waste. For instance, if you have to cut planks of wood that are 3 meters and 4 meters long, the LCM will help determine the most efficient cutting length.
-
Music: The LCM plays a crucial role in music theory, determining when different musical rhythms or melodies will align harmoniously.
-
Software Development: In programming, particularly in tasks dealing with timing or synchronization, LCM plays a vital role in determining the least common timing interval for certain processes.
Extending the Concept: LCM of More Than Two Numbers
The principles of finding the LCM can be extended to more than two numbers. Let's find the LCM of 3, 4, and 6.
Method 1: Listing Multiples This becomes less efficient with more numbers.
Method 2: Prime Factorization
- Prime factorization of 3: 3
- Prime factorization of 4: 2²
- Prime factorization of 6: 2 x 3
The highest power of 2 is 2², and the highest power of 3 is 3. Therefore, LCM(3, 4, 6) = 2² x 3 = 12.
Method 3: Stepwise Approach
You can also calculate the LCM stepwise. First, find the LCM of two numbers, and then find the LCM of the result and the next number. For example:
- Find LCM(3,4) = 12
- Find LCM(12,6) = 12
Conclusion: The Power of a Simple Problem
The seemingly simple question, "What is the smallest multiple of 3 and 4?" unveils a powerful mathematical concept: the Least Common Multiple. Understanding the LCM is essential not only for solving mathematical problems but also for tackling practical challenges across diverse fields. The various methods outlined here – listing multiples, prime factorization, and the GCD method – provide flexible approaches depending on the complexity of the numbers involved. This comprehensive exploration hopefully provides a thorough understanding of this fundamental concept and its significant applications. Remember, even seemingly basic mathematical concepts have far-reaching implications and practical uses in the real world.
Latest Posts
Latest Posts
-
How To Write 200 In Words
Mar 29, 2025
-
What Domain Do Viruses Belong To
Mar 29, 2025
-
What Is The Difference Between The Leading And Lagging Strands
Mar 29, 2025
-
The Si Unit Of Force Is
Mar 29, 2025
-
50 Out Of 60 As A Percentage
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Smallest Multiple Of 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
