What Is The Relationship Between Period And Frequency
Juapaving
Mar 28, 2025 · 7 min read
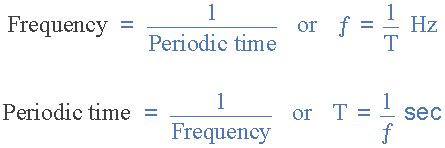
Table of Contents
What is the Relationship Between Period and Frequency?
Understanding the relationship between period and frequency is fundamental to comprehending various wave phenomena, from sound waves and light waves to the oscillations of a pendulum. These two concepts are inversely proportional, meaning that as one increases, the other decreases, and vice-versa. This article will delve deep into this relationship, exploring its mathematical representation, practical applications, and implications across diverse scientific fields.
Defining Period and Frequency
Before examining their relationship, let's define each term precisely.
Period (T)
The period (T) of a wave or oscillation refers to the time it takes to complete one full cycle. Imagine a pendulum swinging back and forth; the period is the time it takes to swing from one extreme point, through its equilibrium position, to the other extreme, and back to its starting point. This is measured in units of time, typically seconds (s). A longer period signifies a slower oscillation or wave, while a shorter period indicates a faster one.
Frequency (f)
Frequency (f), on the other hand, represents the number of cycles completed per unit of time. For the pendulum, it's the number of complete back-and-forth swings it makes in one second. Frequency is measured in Hertz (Hz), where 1 Hz equals one cycle per second. A higher frequency indicates more rapid oscillations or a higher pitch in sound, while a lower frequency suggests slower oscillations or a lower pitch.
The Inverse Relationship: The Formula
The core relationship between period and frequency is expressed by a simple yet powerful equation:
f = 1/T or T = 1/f
This equation clearly demonstrates the inverse proportionality. If the period (T) is doubled, the frequency (f) is halved, and vice versa. This holds true for any type of periodic phenomenon, be it mechanical oscillations, electromagnetic waves, or even the rhythmic beating of a human heart.
Practical Applications Across Disciplines
The concepts of period and frequency, and their inverse relationship, find widespread applications in numerous scientific and engineering fields.
1. Acoustics and Music
In acoustics, understanding period and frequency is crucial for characterizing sound. The frequency of a sound wave determines its pitch. High-frequency sound waves correspond to high-pitched sounds, like a whistle, while low-frequency waves create low-pitched sounds, like a bass drum. The period determines how long a single cycle of the sound wave lasts. The richness and complexity of musical sounds arise from the superposition of multiple frequencies with different amplitudes and periods. Musical instruments are designed to produce specific frequencies, and audio engineering involves manipulating these frequencies to achieve desired sound effects.
2. Electromagnetism and Optics
Electromagnetic waves, including visible light, radio waves, and X-rays, also exhibit periodic behavior. The frequency of an electromagnetic wave determines its energy and type. High-frequency waves, like X-rays, carry high energy, while low-frequency waves, like radio waves, carry lower energy. The period of these waves represents the time it takes for a single complete cycle of the electric and magnetic fields to propagate. Optics leverages the manipulation of light's frequency and period to control its properties, such as color, polarization, and intensity. Spectroscopic techniques rely on the precise measurement of light frequencies to analyze the composition of materials.
3. Mechanical Oscillations and Vibrations
In mechanical systems, periodic motion is common. The simple pendulum, springs, and vibrating strings all exhibit oscillations with specific periods and frequencies. These parameters are crucial in designing structures that withstand vibrations and shocks. Engineers use knowledge of period and frequency to design bridges, buildings, and vehicles that can tolerate various oscillatory loads without structural failure. The understanding of natural frequencies and resonance is essential to avoid catastrophic failures. The natural frequency is the frequency at which a system will naturally vibrate when disturbed, and resonance occurs when an external force applies energy to the system at its natural frequency causing large amplitude oscillations.
4. Electronics and Signal Processing
In electronics and signal processing, periodic signals are omnipresent. The frequency of a signal determines its bandwidth and information carrying capacity. The period is important in timing circuits and clock signals that synchronize the operation of electronic devices. Signal processing techniques often involve analyzing the frequency components of a signal to filter noise, extract information, or modify its properties. Techniques such as Fourier analysis allow complex signals to be decomposed into their constituent frequencies, making analysis and manipulation easier.
5. Medical Imaging and Diagnostics
Medical imaging techniques like ultrasound and MRI utilize high-frequency sound waves and radio waves, respectively. The precise control and measurement of these waves' frequencies and periods are crucial for generating high-resolution images and detecting anomalies within the human body. Understanding wave propagation characteristics and their interaction with tissues is essential for diagnostic accuracy.
6. Astronomy and Astrophysics
In astronomy, understanding the period and frequency of celestial objects' oscillations and waves is critical. The period of a star's pulsation can provide insights into its physical properties. The frequency of radio waves from pulsars helps astronomers understand their rotational speeds and magnetic fields. The analysis of light frequencies from distant stars and galaxies offers crucial information about their composition, motion, and distance from Earth through techniques such as redshift analysis.
Beyond the Simple Equation: Phase and Wave Propagation
While the equation f = 1/T accurately describes the fundamental relationship, a more comprehensive understanding requires considering other factors such as phase and wave propagation.
Phase
Phase represents the position of a point in time (instant) on a waveform cycle. It's usually expressed as an angle (in degrees or radians) and indicates the portion of the cycle that has been completed. Two waves with the same frequency and period but different phases will not be synchronized and could result in interference patterns, depending on the specific phase difference. Constructive interference occurs when waves are in phase resulting in a higher amplitude, and destructive interference happens when waves are out of phase leading to a lower or zero amplitude.
Wave Propagation Speed
Wave propagation speed (v) relates period, frequency, and wavelength (λ) through the equation:
v = fλ = λ/T
Wavelength (λ) represents the distance between two consecutive points in a wave that are in the same phase (e.g., two consecutive crests or troughs). This equation highlights that for a given wave speed, a higher frequency means a shorter wavelength, and a longer period means a longer wavelength.
Advanced Concepts and Applications
The interplay between period and frequency extends into more complex phenomena:
-
Harmonic Motion: Many real-world oscillations are not perfectly sinusoidal but contain multiple harmonic frequencies – multiples of the fundamental frequency. Fourier analysis is instrumental in decomposing complex waveforms into their harmonic components.
-
Resonance: As mentioned earlier, resonance occurs when a system's natural frequency matches an external driving force's frequency, leading to amplified oscillations. Understanding resonance is crucial in various engineering applications to either avoid or exploit this phenomenon.
-
Wave Interference and Diffraction: The superposition of waves with different frequencies and periods leads to intricate interference patterns. Diffraction, the bending of waves around obstacles, is also profoundly influenced by frequency and wavelength.
-
Signal Filtering: Filtering techniques in signal processing manipulate signals by selectively attenuating or amplifying certain frequency components based on their periods.
Conclusion: A cornerstone of Physics and Engineering
The relationship between period and frequency is a fundamental concept that underpins our understanding of oscillatory and wave phenomena across numerous disciplines. From the subtle vibrations of a musical instrument to the vast expanse of the cosmos, the inverse relationship between period and frequency provides a crucial framework for analyzing, interpreting, and manipulating these phenomena. Mastering this relationship is essential for anyone pursuing studies or careers in physics, engineering, medicine, and many other fields that engage with the behavior of waves and oscillations. By continuing to delve deeper into these concepts and their implications, we unlock a more comprehensive understanding of the physical world around us.
Latest Posts
Latest Posts
-
Equation Of A Circle Calculator Given Two Points
Mar 31, 2025
-
What Is The Least Common Denominator Of 8 And 12
Mar 31, 2025
-
5 Letter Words With Er In The End
Mar 31, 2025
-
What Are The Common Factors Of 28 And 36
Mar 31, 2025
-
What Is 6 10 As A Percentage
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Relationship Between Period And Frequency . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
